用数学来保护民主(搬运整理一些关于gerrymander的讨论)
【本文内容是基于Harvard Data Science Journal的创刊会议,视频在这里,介绍在这里。 会议上午是讨论美国人口普查中的隐私问题,下午就是讲美国的选区划分不公平问题(选区划分需要基于人口普查数据),或者说gerrymander。个人感觉这部分有些意思,就做一下搬运。如无特别说明,配图均来自于讲者的ppt】
gerrymander的历史和名词来源我就不介绍了,中文和英文wiki有足够详细的内容。这个概念的大意就是,通过不公正的选区划分方法,使得某些党派获得远超其票数的议会席位——猫党如果想赢得更多的席位,就要在选区划分上尽可能地把狗党的选民集中到同一选区,然后让自家选民能够在尽可能多的选区内占到多数票。
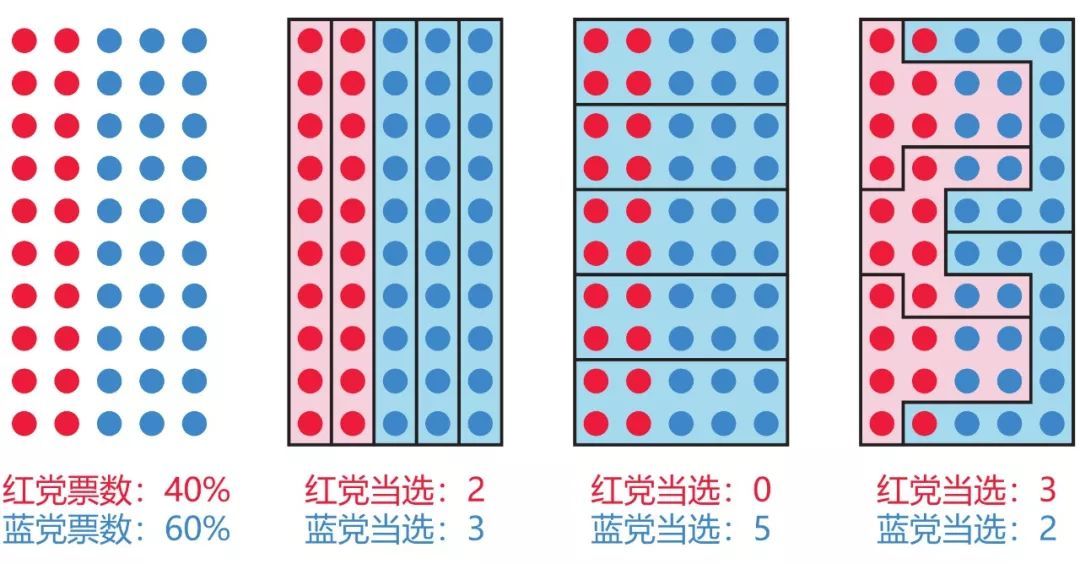
Gerrymander是一个在美国相当普遍的现象,不少的州都有各种荒唐或者巧妙的选区地图设计,浪费掉某党的选票使其没法获得与民意相称的席位。
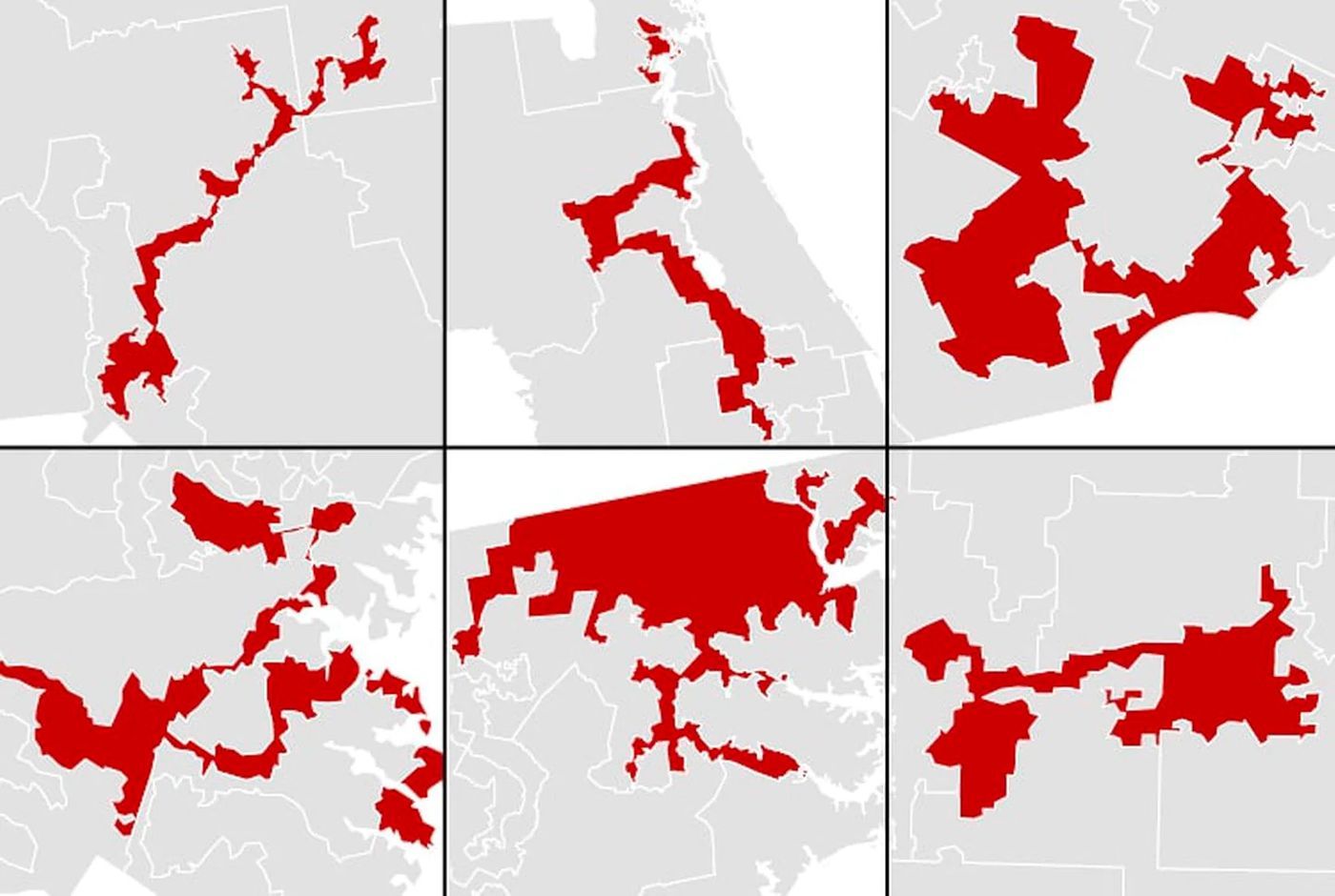
毋庸置疑,Gerrymander当然是反民主的,甚至可以说这个在全是美国政治体制中最亟需解决的bug之一。曾见过一个一针见血的评价是,这不是民众在选择政客,而是政客在选择民众。
美国各界现在已经在严肃对待这个现象了,且都在采取行动解决。比如,宾州法院就曾经判决要求宾夕法尼亚必须重新划分选区,不过今年联邦法院就判决自己并不能干涉各州的选区划分。不过,司法上的争议是一方面,但要解决gerrymander的话,一个现实的问题就是,什么样的选区划分是不公平的,而怎么划分选区才是公平合理的?
人们看到gerrymander地图时,会下意识地觉得,这种地图形状过于离奇的选区就是不公平的。不过麻烦的是,除了某些过于明显的形状,人们很难凭借肉眼来判断两种不同的选区划分谁更公平。Wes Pegden以宾州改革时考虑的不同地图为例,来证明直觉在这个问题上并不是一个好的标准。
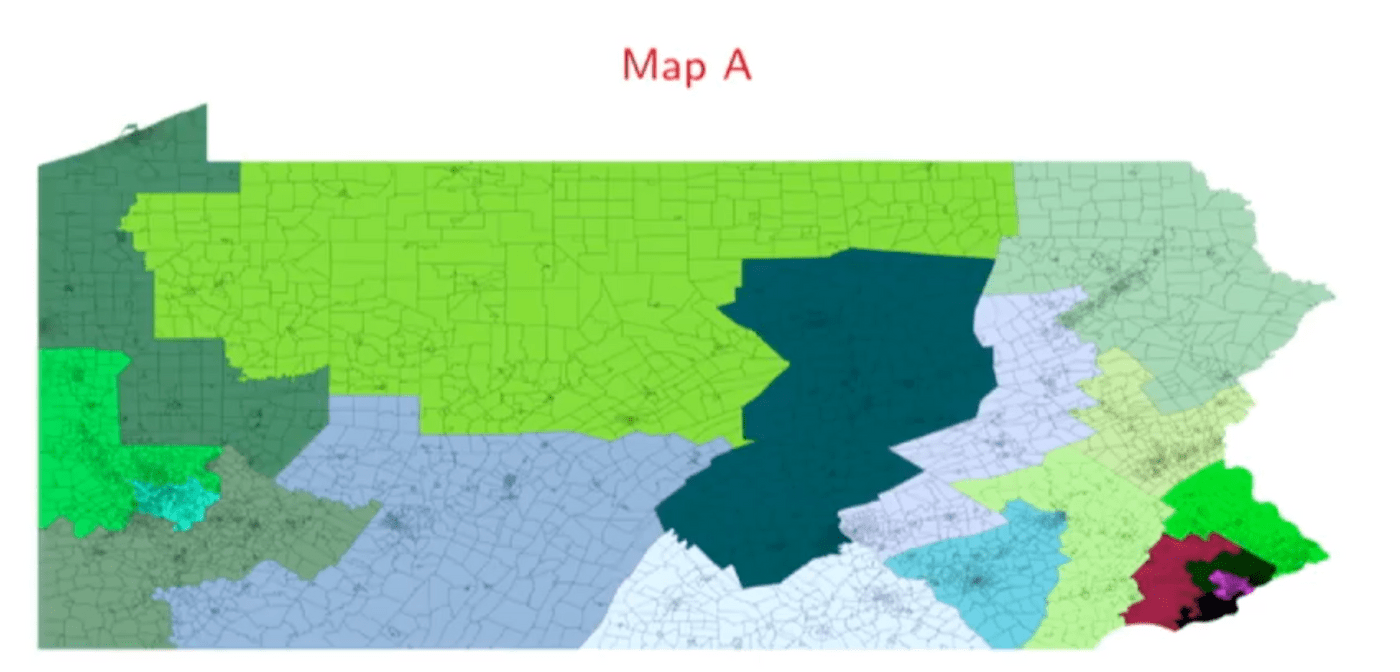
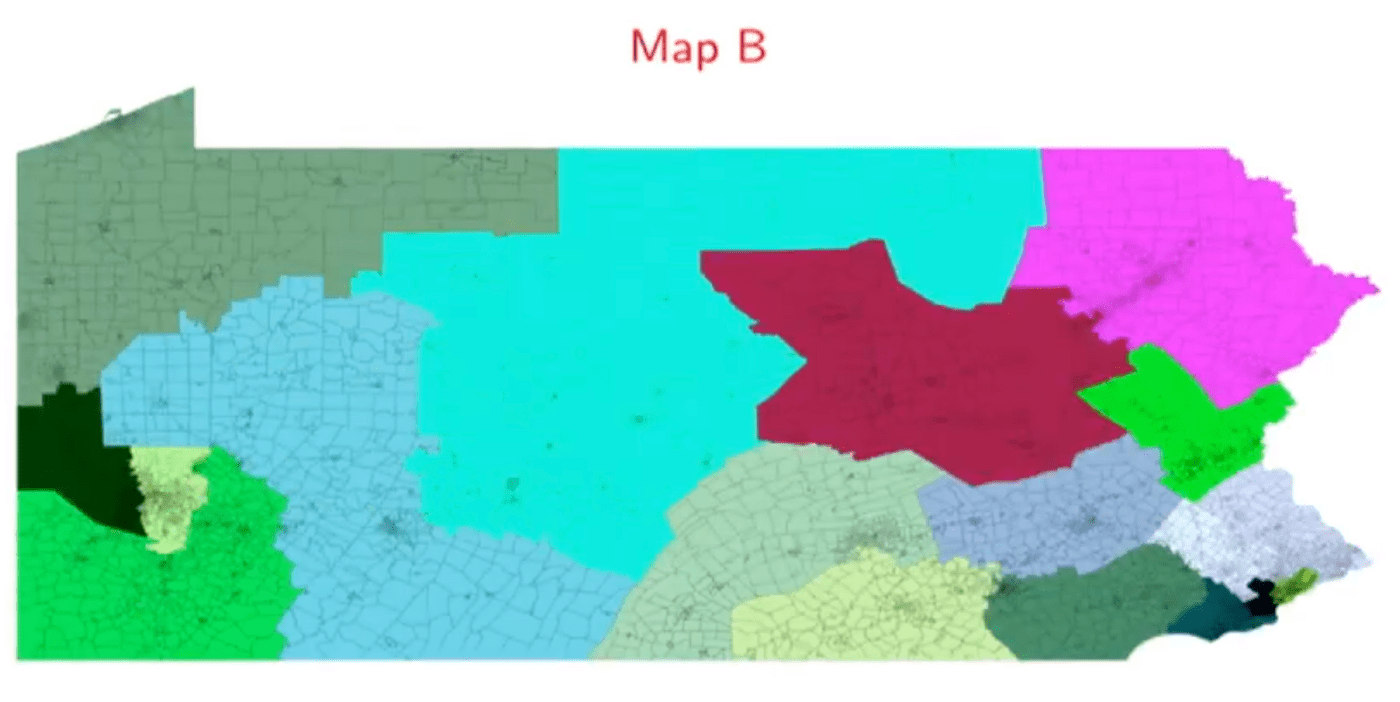
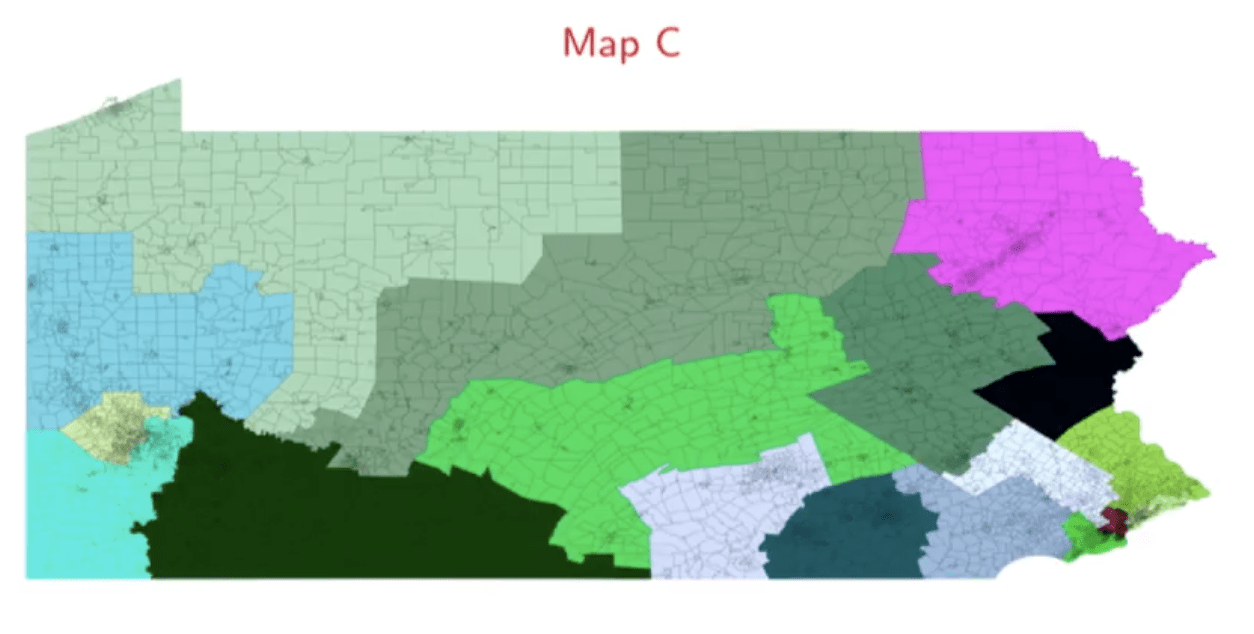
所以,选区划分问题就一定需要科学的方法来量化和解决。图形的紧凑程度(compactness,我不太清楚其数学定义)自然会被人们首先想到。Dustin Mixon 还介绍了一个叫做Polsby-Popper score的测量方法,其核心就是考虑图形的面积和周长的比例。直觉上,我们确实会觉得那些长得七倒八歪的选区都不会有很高的compactness,面积与周长的比例也会相对很低。这样似乎能够找出那些gerrymander的地方?当然不会这么容易的。因为这些方法其实是会遇到不小的假阳性(false positive)和假阴性(false negative)问题的。
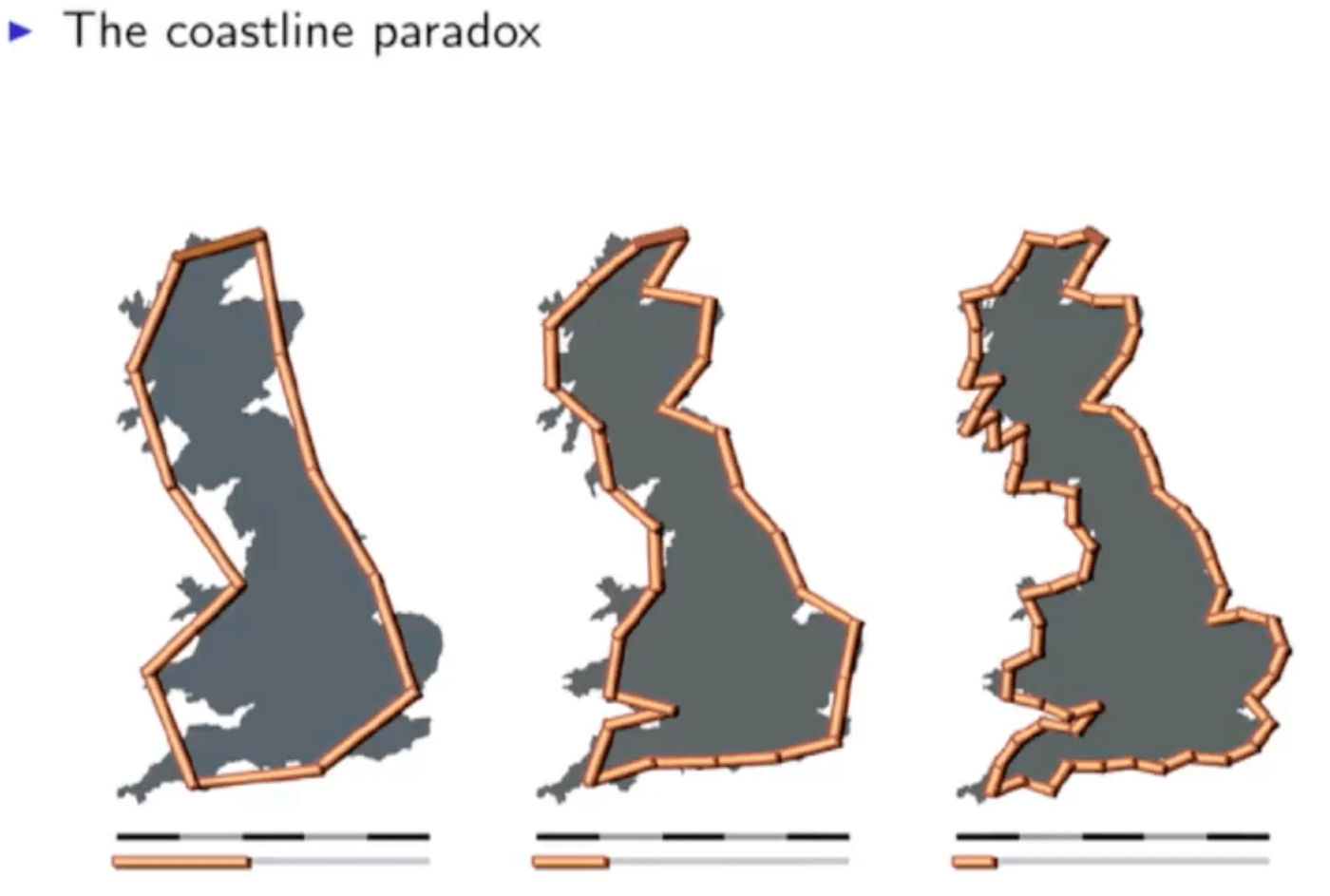
首先是假阳性问题,也就是说把不是gerrymandering的地方当作了gerrymander。Dustin第一个论点是是coastline paradox(海岸线悖论):现实中一块不规则形状地域的测量周长,可能会因为尺子本身的长度而变化。如下图的英国地图所示:
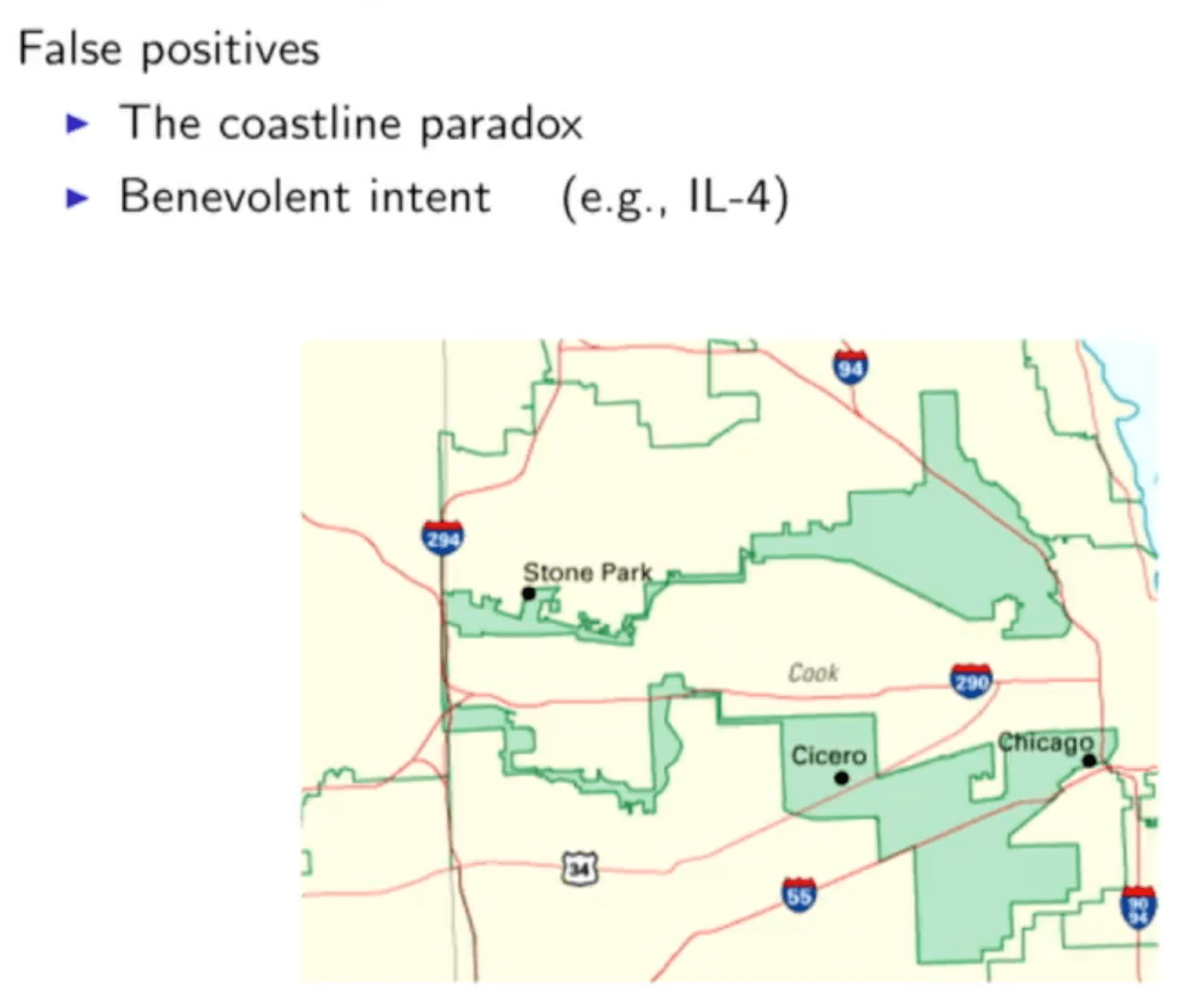
而第二个论点是,有时候长得奇怪的选区不一定是因为gerrymander形成的。他以伊利诺伊州的两个选区举例,它们看起来真的很奇怪,太像gerrymander了。但Dustin说,其实不然,虽然这些选区是故意被划成这样的,但原因不是党派利益,而是为了尊重当地的文化(我并不了解具体的背景)。这附近全是民主党的基本盘,所以其实没人因此受损反而是一场皆大欢喜的事情。
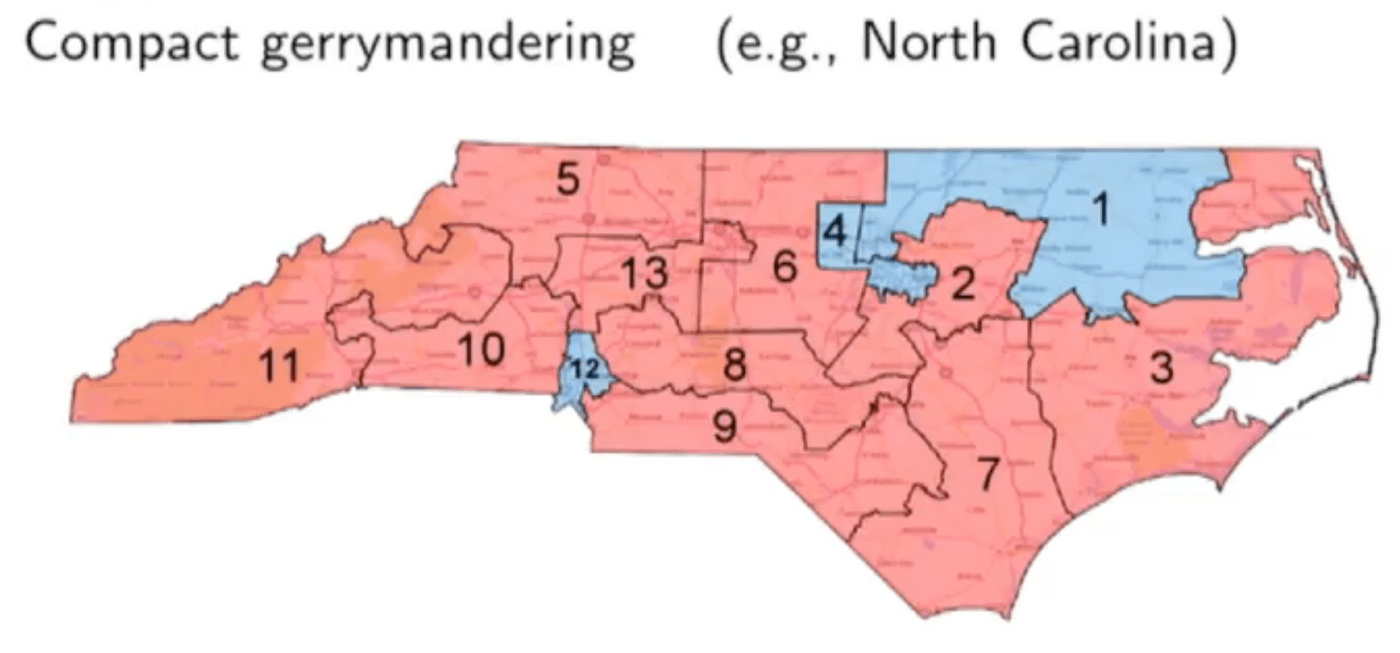
而对于那些看起来比较紧凑的地图,其实也可能是gerrymander,这就是假阴性问题。在现实中的例子就是北卡。在这个州里共和党能拿到近50%的选票,却能够取得13席众议员中的9席。
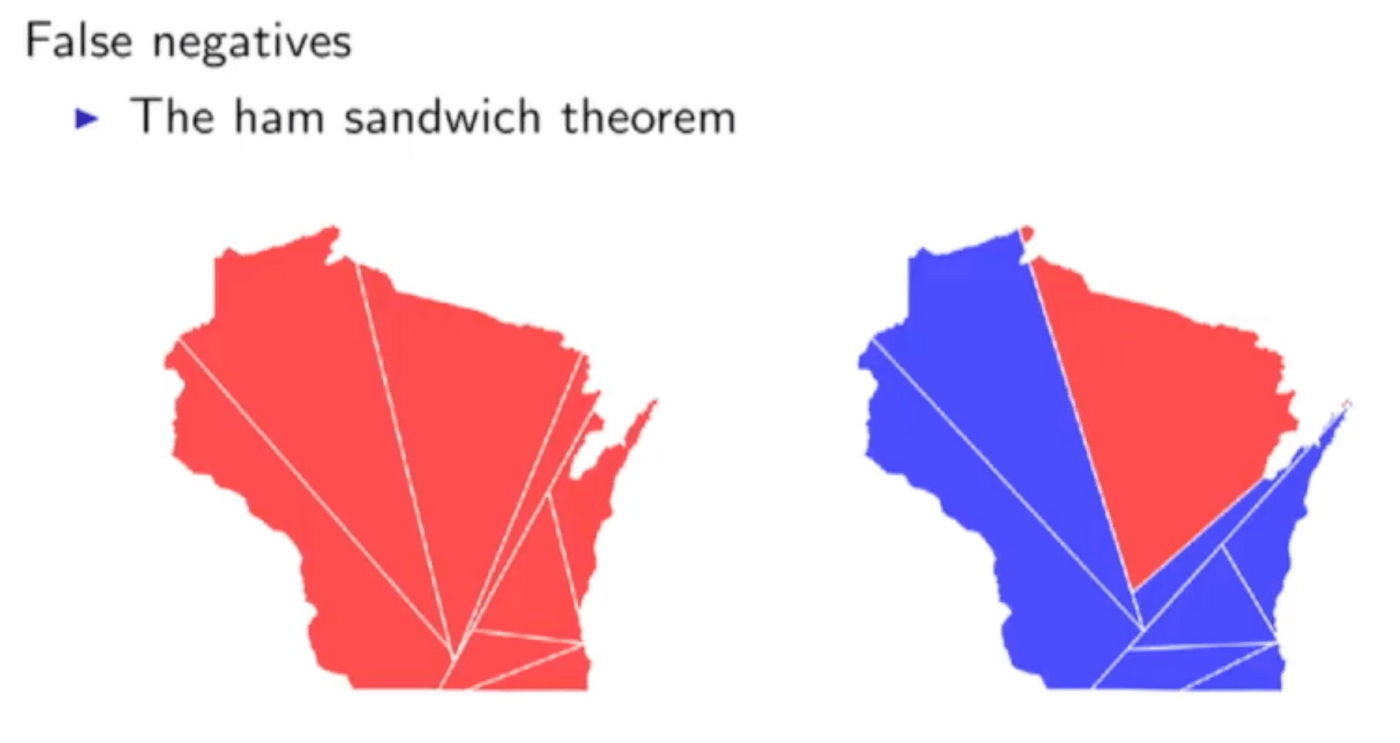
甚至,他以Wisconsin州的选举数据为例,用电脑做了模拟——哪怕选区的划分是看起来非常公平的直线,形成三明治一样的形状,也可能带来完全不同的结果……
Moon Duchin 也认为类似于compactness这类经典方法相当有问题(deeply flawed)。她介绍了efficiency gap作为判断是否出现gerrymander的指标。这个方法的大意就是考虑有多少选票其实是被浪费在了输家身上,有多少(在保证获胜后)多余的选票被浪费在了赢家身上。Moon介绍说这个方法确实相对有效,但也有不少的问题,比如在密苏里州和犹他州实践起来会有很难按标准合理划分选区或者怎么都无法扭转gerrymander的情况。NYT也有文章写过,这种方法本身并不能区分gerrymander还是自然的选民集中——在大城市,被浪费的选票自然会多一些。
更让人头疼的是,Wes Pegden 告诉大家,即使你直接去看选票数和席位数,也不一定能够确定出是否真实存在errymander。他以宾州的选举数据为例,让计算机随机划分出一些地图,但还是很容易让共和党在50%的选票总数上占到席位的绝对优势。
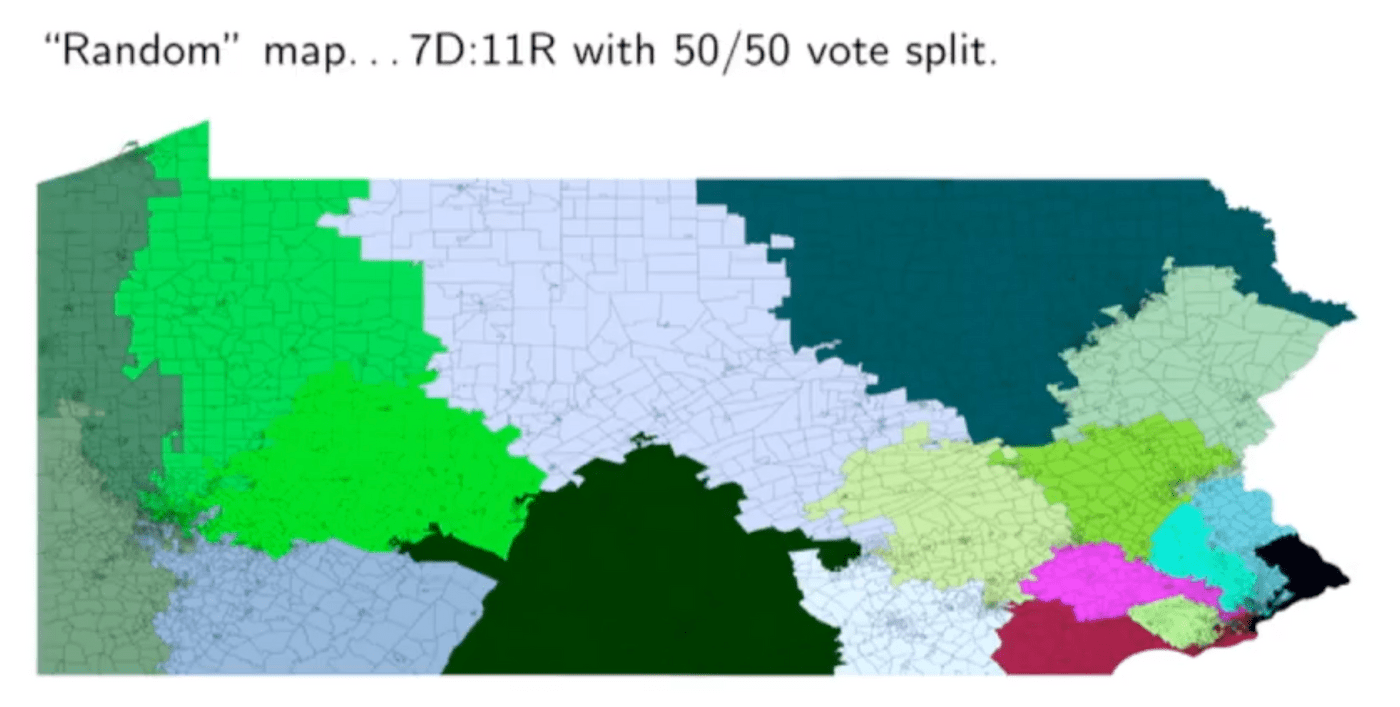
于是,Wes就换了个思路,不是看选区地图本身是否是gerrymander,而是看选区地图本身有多大可能是被精心设计过(carefully crafted)。他用Markov链来在已知地图上反复尝试随机改变某个小地方(eg. county)的选区归属,然后根据选举结果来预测这个地图有多大程度上被精心设计过,也就是被故意gerrymander了——举例来说,只有0.00002%的随机生成地图不比Wisconsin当前的选区地图公平……
对这种方法的最大顾虑来自于,它有多大可能带来假阳性。或者更复杂一点的说法是,随机地图的党派倾向是否会在随机改变下持续地改变。Wes的研究(1,2)证明(对不起,没完全看懂,所以)简单地说,不会。在假设检验下,假阳性是一个可控的问题。
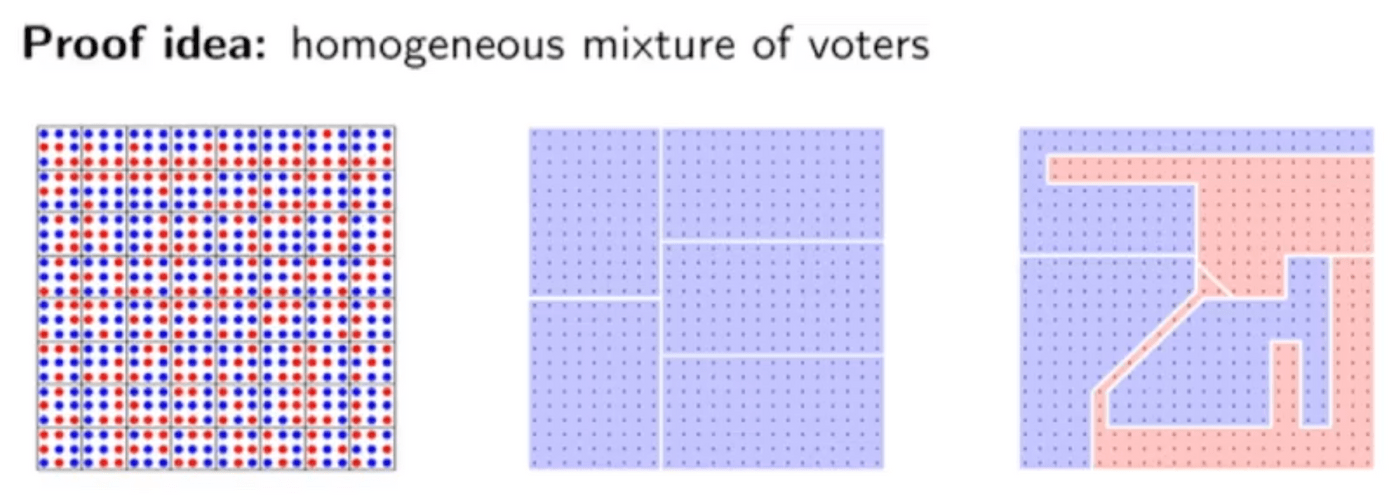
比起探测出gerrymander,更困难的问题应该就是怎么画出一个公平的选区地图,虽然后者是一定需要建立在前者的基础上的。Dustin强调,选区划分需要满足一个基本的标准,比如政党的席位比例应该大致近似于选票比例,这样才能算是民意的代表。然而,这种要求并不容易满足。他随机生成一张地图,让蓝方有着一点点优势。但在这个地图上,要让五张选票相对符合比例地代表红蓝的选票分布,选区划分反而需要非常的异类……
在现实当中,类似的例子恐怕就是麻省了。这个深蓝的州里有30%左右的人在2016年大选中投了Trump,或者说偏向于共和党,但现在麻省九个众议员席位都被民主党获得了……something weird here
最后,Dustin还表示,即使一个公平的选区地图确实存在,要找到它也是一个NP-hard问题(通俗地讲,相当相当难)……当然,他也安慰大家,没必要太悲观,因为他们主要是讲的最糟糕的情况,虽然各种方法都有着自己的优劣,但在现实世界里找到一个合理的地图多数时候没有困难。毕竟,选区划分其实并不需要达到数学意义上的最优,只需要大致不错就可以了。
Bridget Tenner讲了一个和gerrymander关系不大,但同样是选举的问题。作为一个数学家,她同时也关注怎么合理的可视化选举结果。传统的一人一票投一个候选人的选举很简单,但ranked-choice vote(选民需要将候选人排序)应该怎么展示才对?澳大利亚、爱尔兰、缅因、佛蒙特、旧金山都有这种投票方法。
Ranked-choice vote的计票方式不只一种。Bridget讲的是instant-runoff voting,即在计票时,每一轮排除掉一个获得最低(第一)选票的候选人,然后将那些选票上的候选人全部上移一位。这样反反复复,直到某个候选人获得多数票。
Bridget以缅因州第二选区的结果为例说,媒体不仅没有很清晰地向读者说明某人是怎么就赢了,而且在这种相对复杂但信息量更大的选举系统下,没能成功传递出“哪些人是某人的胜选基础”这种信息。
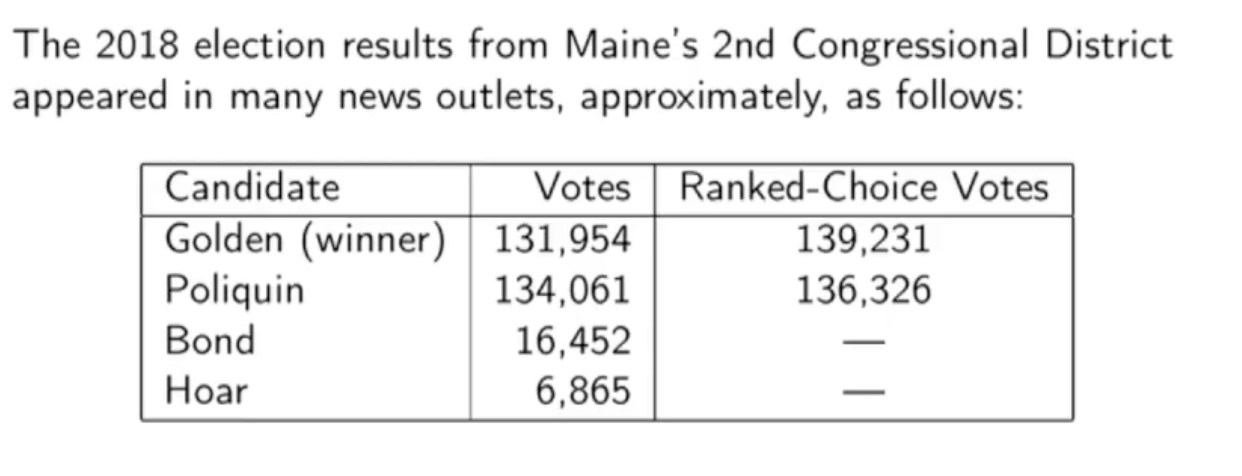
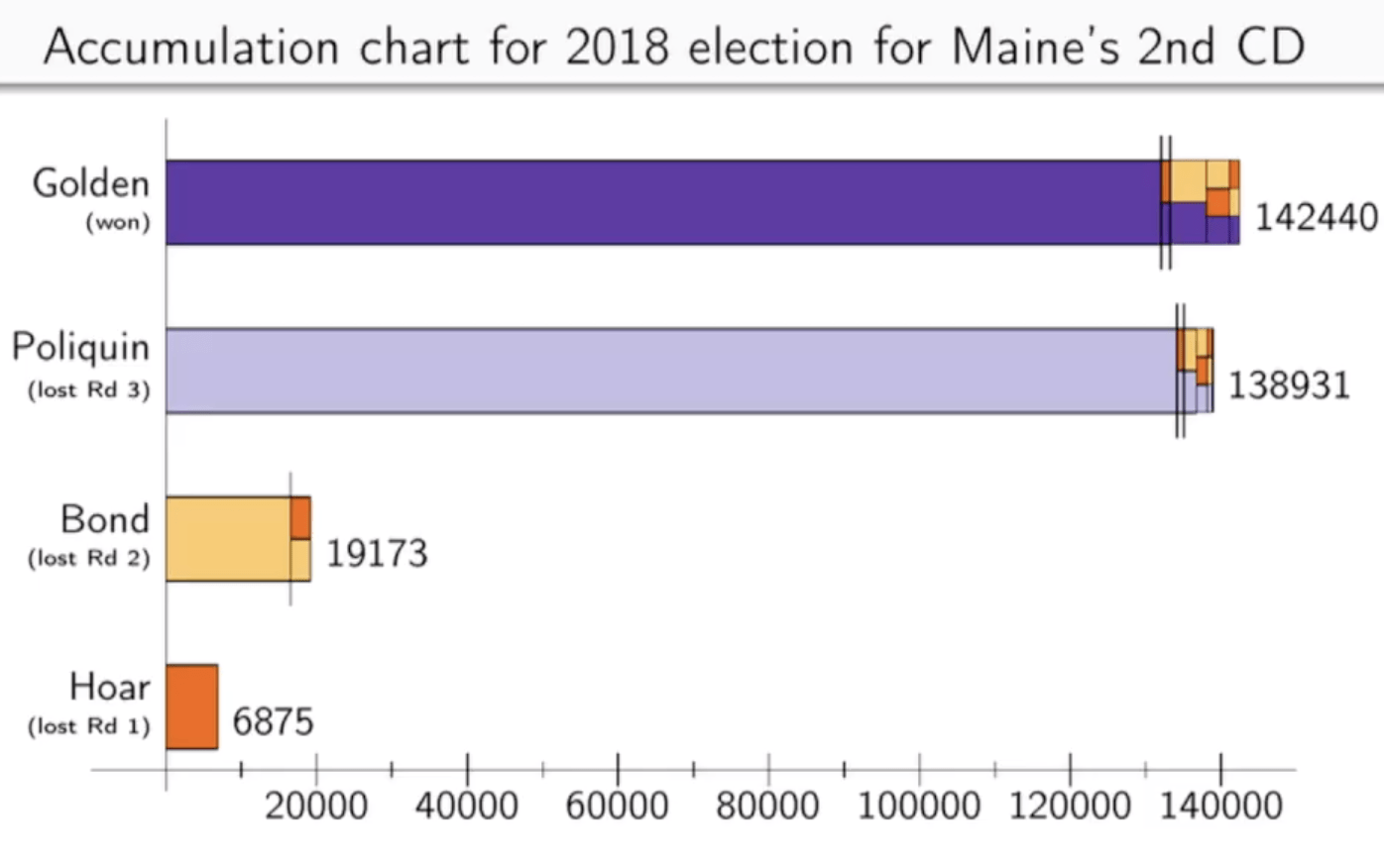
于是,Bridget就在累积图表(accumulation charts)提出了一个新的选举结果可视化方法,如下图所示。如果读者要看谁最终赢了,只看条形的长度即可;如果读者想要知道某个候选人是具体怎么赢下来了,什么投票帮助获胜的,就可以更为细致的看条形的颜色。
这幅图里,所有候选人的基础投票(排序第一的投票)就是竖线前的数据,每一次竖线代表着(排除掉最低票数候选人的)一轮。所以,在第一轮后,Hoar被排除掉了。然后那些在 把Hoar排在第一位的选票 上的第二候选人会随之获得这些选票。以Bond为例,竖线后面的双色块,其高度没有真实意义,但是宽度代表了有多少选票是 把Hoar排第一,把Bond排第二。所以如果某个选民的选票是把Hoar 排第一,Bond排第二,Golden排第三,那么这张选票对应的小色块(从上至下)就分别有橙色、黄色和深紫色。在这种表示方法下,参选的人能够清晰的看出民意偏好的分布是什么样的,自己应该去找谁拉票。
我本身没有研究过gerrymander,只是对此特别感兴趣。之前听到Gary King讲过他针对gerrymander的研究。另外,普林斯顿大学的Sam Wang也是以研究gerrymander出名的学者。了解不多,欢迎大家补充。

后记: 1. 政治地理学,其实在很多地方都有,包括中国。像中国这样省份边界犬牙交错,有时候极为突兀的现象,在很大程度上也是古代统治者为了制衡地方而故意这么设计的。即使没有选举,也有权力 2. 怎么样才能让议会合理地代表民意,这是代议民主制里的一大难题。而我个人不觉得美国的选举制是典范,这种赢者通吃的制度弊端蛮大的(有很多讨论了,我就不赘述了) 3. 因为即使在香港这样不算民主制的政体里,民意代表问题也极为突出,甚至在某种程度上就是这几个月抗议的诱因之一(参加《香港第一課》18. 為什麼特首選舉會被批評為假選舉?) 4. 民主是一个细节丰富的制度问题,不是自己拍着脑袋就能弄清楚的 5. 互联网上的同温层/回音室(echo chamber),在不少人看来,也是一种数字世界里的gerrymander