Machine Learning - 給自己的機器學習筆記 - Linear Regression - 迴歸模型介紹與公式原理教學
Yo~ 今天我們來學不管大家是想學機器學習,還是想學統計,來對我們的資料進行預測與分析,都會用到的線性迴歸模型,它是一個非常重要的分析數據的方法,也很酷很有趣喔,那我們來一起開始吧
迴歸模型要做什麼用 與 原理是什麼?
1. 迴歸模型在做什麼事?
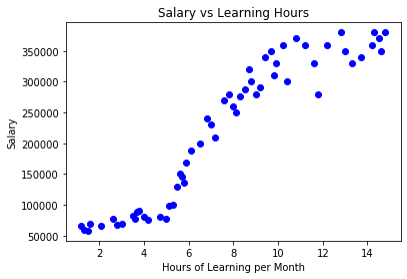
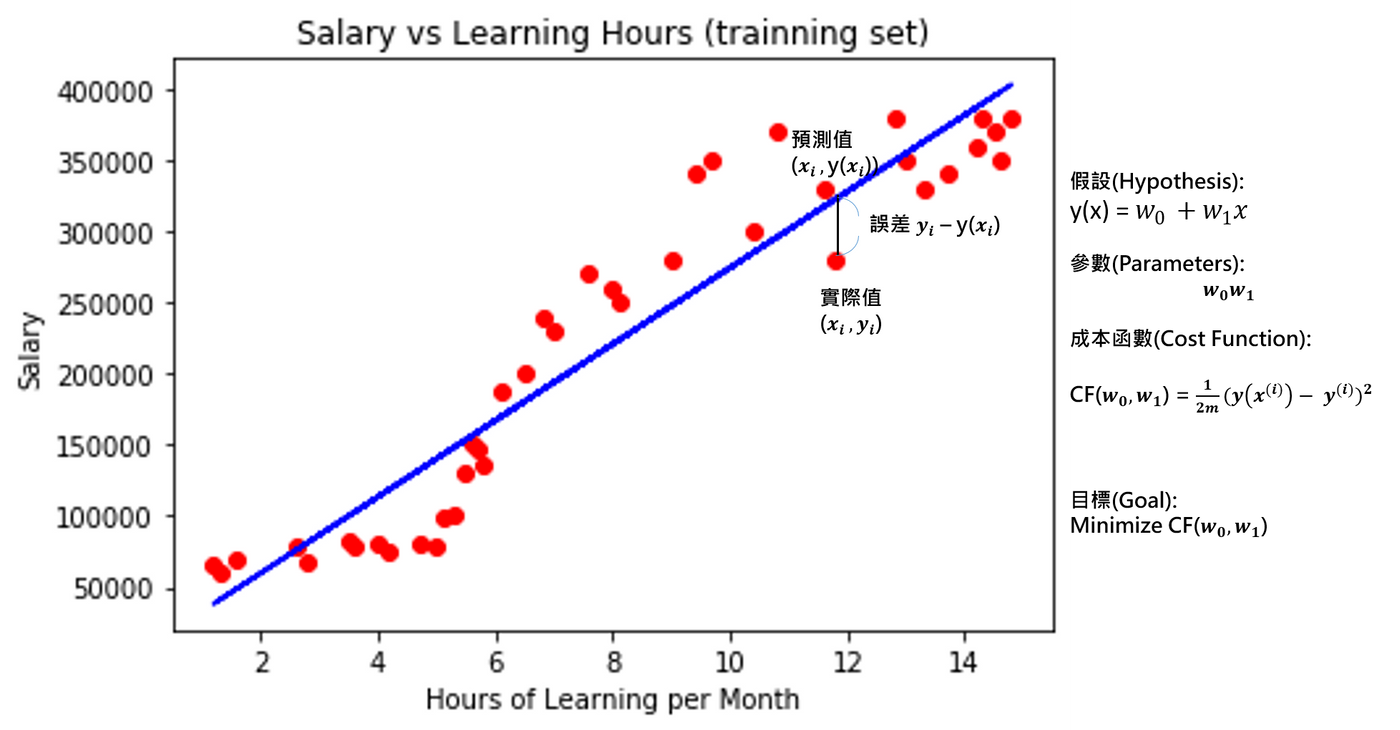
這邊有一個我捏造的數據集,如圖一,x軸為每個月的學習時數,y軸為薪水,而這些數據點為數據集中的每一筆數據資料,而經過迴歸模型訓練運算後,我們會找到一條如圖二的線,它像是從這些數據點位置的中間穿了過去的線,透過計算出這條迴歸模型線的方程式,我們就能預測新的數據點,舉例像是今天來了一個新的人(新數據點),我們得知他的學習時數(自變數),就能夠預測他可能的薪水(應變數)
圖一:數據集
圖二:迴歸模型與數據集的關聯
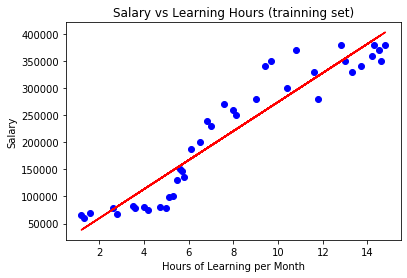
小提醒: 圖二大家可能有疑問說為什麼數據比較少,我會在下一篇的實作教學中跟大家講解XD,其實簡單來說,就是這邊是訓練集的模型預測結果視覺化圖
2. 我們如何計算出這條線的方程式呢?
透過最小平方法來計算並建構出迴歸模型,計算出一條方程式,視覺化出一條迴歸線,使這條迴歸線與所有的數據點的距離並不會相差太多,也就是在有同樣的X軸值下,y軸值不會相差太多,也就是實際點與線的距離誤差不會太大,根據我們的數據簡單來說,就是在同一學習時間值(自變數)下,預測出的薪水(應變數)不會誤差太多
3. 如何找到最佳的線方程式?
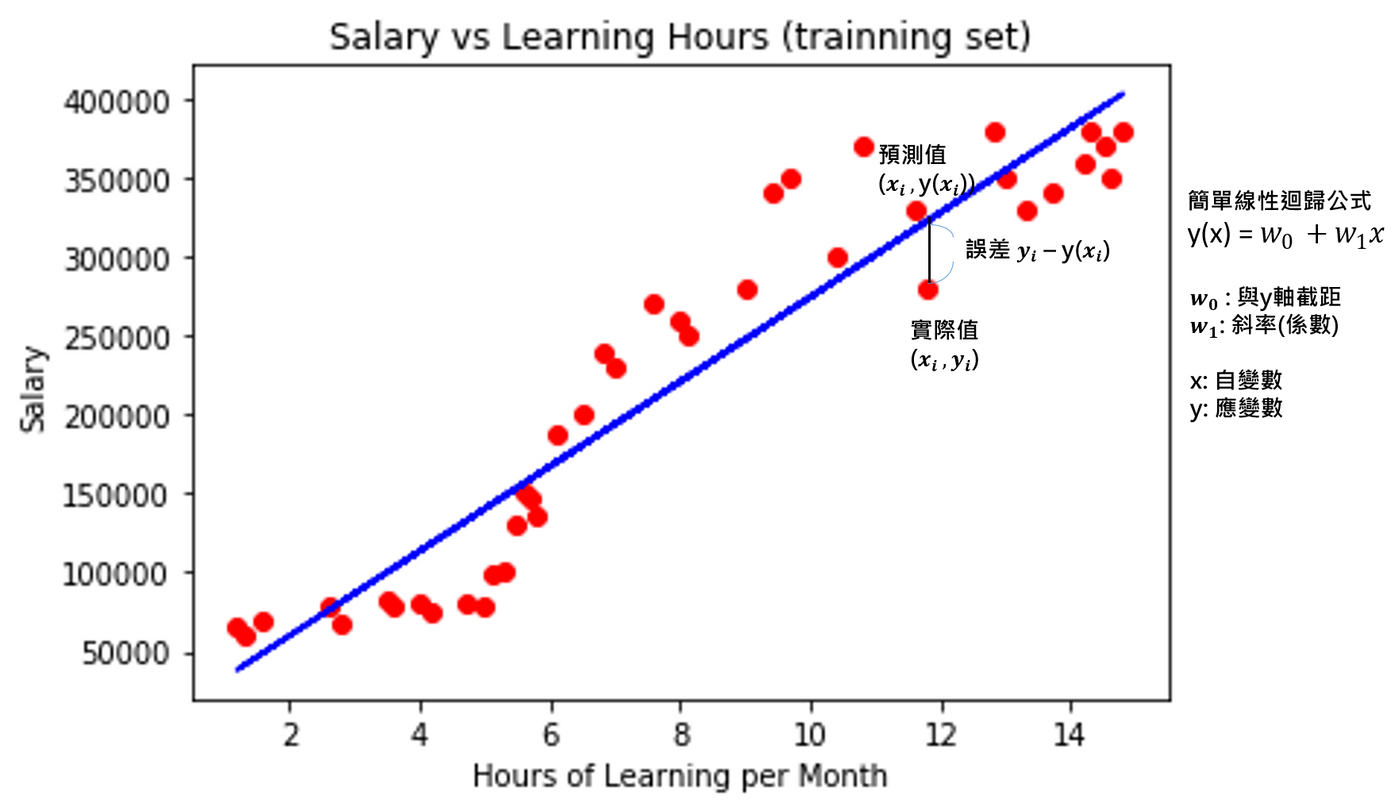
實際數據點(值)與這條迴歸模型線相切的點就為迴歸模型的預測值,如圖三,這條相切的直線就是它與實際點的距離差,也就是預測值與實際值的誤差,加總這些實際點與預測點的誤差的平方,就能計算出成本函數(Cost Function),或稱損失函數(Loss Function),如圖四的公式,並且想辦法讓成本函數最小化,就能找到最佳的一條迴歸模型方程式喔
圖三: 為了方便講解,圖是以簡單線性迴歸(Simple Linear Regression)為例子喔,所以方程式才會只有這樣,線也才會只有直的XD
圖四: 我們會利用最小平方法來計算出那條迴歸模型線,而這些點與線的距離和,就是誤差和,算法就稱為成本函數(Cost Function),或稱損失函數(Loss Function)
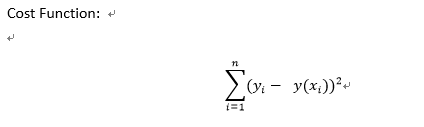
補充 圖五:是我根據網路上找到的資料重新繪製的視覺圖,它清楚的呈現了如何計算出迴歸方程式的方法,跟我上面的成本函數公式有一點點的不同,為了方便與大家講解,所以我踩用了我在看教學文章中,最好理解的公式,如圖四
4. 如何最小化(Minimize)成本函數(Cost Function)?
使用梯度下降(Gradient Descent)!!
要最小化成本函數(Cost Function),也就是讓實際點與迴歸模型上的預測值誤差最小化,而影響這條迴歸模型線有一個重要的因子,就是斜率,所以我們需要計算出這條迴歸線的截距與斜率,也就是找到如圖三的W0與W1,也就是計算出權重值,而簡單的線性迴歸,可以使用聯立方程式求解或線性方程式解(Normal Equation)來找最佳解,但現實中有相當多種的迴歸模型,也就有相當多種複雜的方程式,我們就不可能都用上述兩種方法,來計算複雜的方程式,這時就需要梯度下降(Gradient Descent)的方法來協助我們,以最快速的方法找到最佳解(極值)
5. 梯度下降(Gradient Descent)方法是如何運作的?
梯度下降(Gradient Descent)最有名的解釋方式,就是爬山的故事,想像一下我們人在玉山的山頂,並且思考著要如何最快回到山底呢,總不能直接跳下去吧,那太陡了XD,而我們就要挑選很陡的坡來走,才能最快下山,而這個陡坡的傾斜程度,就是利用成本函數進行微分得來的,而乘上的α係數,就是學習率(Learning Rate),代表著我們走一步的距離,但是設定α係數千萬不要覺得越大越好,太小會很慢才到山底,而太大一開始確實會幫助我們下降很快,但因為每一步的距離太大,會讓我們過頭,想像一下有一個U型谷,每移動一次我們就要找尋最佳切線(傾斜程度),然後移動一步距離(α係數),如果移動太大就會超過山底,很難剛好走到山底的位置,也就很難找到極值(最佳解)
梯度下降(Gradient Descent):根據對成本函數(Cost Function)進行運算處理,並計算出新權重值(極值)的公式
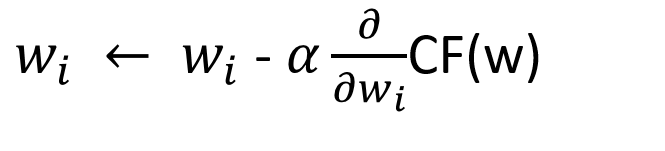
公式講解: 對成本函數進行微分(Cost Function),並乘上學習率(alpha),並拿上一次更新的權重值減掉它,成為新的權重值(極值)
疑問:為什麼是用上一次計算出來的權重值減微分後乘以α係數(學習率)的成本函數(Cost Function),成為新的權重值呢?為什麼不是用加?簡單來說,想像一下,因為我們要不斷逼近山底,也就是方向是往切線的下方走,所以是用減的喔
重點整理
我們要最快下山,也就是要以最快的方式找到極值,取決於選擇路線的陡峭程度與每一步距離
- 陡峭程度(切線斜率): 對成本函數(Cost Function)進行微分
- 每一步的距離: α係數,也就是學習率(Learning Rate)
- α係數設定太小,走太慢(找尋極值太慢),設定太大,一步距離太大,很難剛好走到山底,這就是所謂的震盪
補充:梯度下降(Gradient Descent)方法有哪些 與 它們在找尋權重值(極值)的公式差別
1. Batch Gradient Descent (批量梯度下降法):
- 以簡單線性迴歸為例,就是每次運算新權重值時,也就是調整產生新的w0與w1時,都會計算到所有的數據點(樣本)
- 優點:精確度(Accuracy)很高
- 缺點:計算成本龐大
2. Stochastic Gradient Descent (隨機梯度下降法):
- 以簡單線性迴歸為例,就是每次運算出新的權重值時,也就是調整w0與w1時,只會計算一個數據點(樣本)
- 優點:計算成本非常低
- 缺點:精確度(Accuracy)沒有那麼高
3. Mini-Batch Gradient Descent
- 綜合前面兩個梯度下降方法,以一些樣本來計算,並調整新的權重值
小筆記:簡單來說,就是Batch Gradient Descent每次計算並調整新的權重值時,都需要動用所有的數據集樣本,而Stochastic Gradient Descent只動用一個數據集樣本,而Mini-Batch Gradient Descent,則綜合兩者以一些樣本來計算調整
詳細的梯度下降(Gradient Descent)方法,我會在之後學習,並分享給大家學習
補充:線性方程式解(Normal Equation)與梯度下降(Gradient Descent)方法,找尋最小化(Minimize)成本函數(Cost Function)的步驟
1. 線性方程式解(Normal Equation)步驟
Step1: 定義成本函數(Cost Function)
Step2: 對成本函數(Cost Function)微分求極值,也就是我們要的權重值(補充:方程式進行微分的時候,在零的點上,可以找到最大或最小值,也就是極值)
Step3: 找到權重值
2. 梯度下降(Gradient Descent)步驟
Step1: 隨機初始化權重值,也就是先隨機找值當權重值
Step2: 利用微分成本函數(Cost Function)的方式,沿梯度相反方向下降求極值,並根據學習率大小(α係數,Learning Rate),調整下降一步距離
Step3: 重複Step2,直到找到最小化的成本函數(Cost Function)
Step4: 計算並找到權重值
迴歸模型種類與公式
簡單來說,迴歸模型是用來瞭解自變數與應變數之間的關係,縱而未來有新樣本加入數據集時,我們有它的特徵(自變量),就能預測它應變量的值,而根據每個數據集的特徵維度不同,也會有不同計算方法的迴歸模型,大致可以分成以下幾種迴歸模型:
1. 簡單線性迴歸(Simple Linear Regression)
- 說明:就是我們這篇一直使用的範例圖(如圖二),所計算並繪製出一條直的迴歸線,它代表著特徵(自變數)與目標(應變數)之間的關聯
- 使用時機:特徵(自變數)與目標(應變數)的關係呈線性關聯
- 公式:
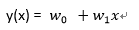
2. 多項式迴歸(Polynomial Regression)
- 說明:簡單線性迴歸(Simple Linear Regression)只能找出線性的關聯,但有些數據並非線性的,就要使用能夠計算非線性的高維度多項式迴歸(Polynomial Regression)模型
- 使用時機:特徵(自變數)與目標(應變數)的關係呈現非線性
- 公式
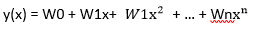
3. 多元迴歸(Multivariable Regression)
- .說明:數據集的特徵通常不只一個,多特徵同時影響目標的情況,也就是多個自變數同時影響應變數的情形,就適合使用多元迴歸(Multivariable Regression)來建立模型
- .使用時機:特徵數量(自變數)多,且對目標(應變數)都有影響的時候
- .公式
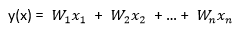
建構迴歸模型可能遇到的問題? 過度擬和與低度擬和
選擇參數數量是一門藝術,非常重要!!數據集中的特徵數量的選擇也非常重要,總不能所選的特徵比樣本數量還要多吧,像是我要收集很多人的特徵(身高、體重、三圍等等)來預測薪水,但我的數據集只收集了兩個人(樣本)的特徵資料
低度擬和
- 訓練出來的迴歸模型,沒辦法描述數據集資料,也就是沒辦法解釋問題的複雜度,使得整個預測效果很不好
- 當選擇的參數太少,以至於迴歸模型的預測效果相當不好
- 舉例來說,就是實際狀況下影響應變數(果)的自變數(因)有很多種,應該要用多項式迴歸模型來計算,但我們卻用只用一個自變數來預測應變數的簡單線性迴歸模型,來計算,導致敬效果不彰
過度擬和
- 訓練出來的迴歸模型,過度地解釋問題的複雜度,導致過度的符合這次的訓練集資料,這樣有新的樣本加入後,預測的效果並不好
- 當選擇的參數過多,以至於迴歸模型在預測這次訓練模型用的數據集,表現的效果相當精準,但實際去預測新的數據時,準確率卻突然不高了
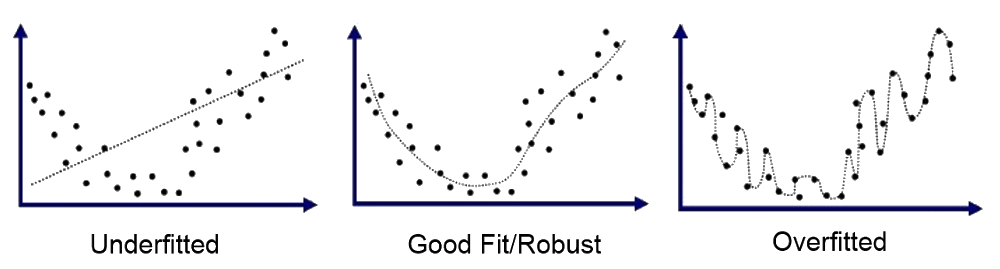
如何降低過度擬和?
過度擬和的問題來自於我們選擇的特徵數量太多,造成明明是類似的特徵,但因為都被我們拿來當自變數訓練迴歸模型,導致有了加成的效果,也就是所謂的特徵共線性問題,舉例來說,我們想預測國中生中未來會考上第一志願的機率,我們拿了許多的特徵來訓練模型,像是是否資優班、數學分數、考試平均分數等,來進行預測,但只要他是資優班,他的數學分數就容易是高的,而他的考試平均當然也有很大的機率是高的,它們三種特徵明明就具有關聯性,卻被當不同的特徵來訓練,這樣就很容易造成所謂的特徵共線性問題,導致三個特徵的加成加重了效果,影響了最後成果的模型預測能力
- 解決方法 提供一個懲罰機制,來降低用以訓練模型的特徵使用量,以降低過度擬和的問題,這樣的方法稱為正規化,如下述兩個方法:
1. Lasso Regression (L1)
- 說明:我們讓成本函數加上懲罰項,並且要盡可能的最小化這個加起來的值(如下公式),但大家也看到了,如果我們加入越多的特徵(n),也就是將權重值取絕對值相加,右邊的懲罰項就會越大,就很難最小化,藉此來控制特徵的使用量不可以太多
- 公式
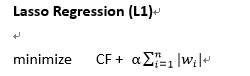
2. Ridge Regression (L2)
- 說明:我們讓成本函數加上懲罰項,並且要盡可能的最小化這個加起來的值(如下公式),但大家也看到了,如果我們加入越多的特徵(n),也就是將權重值平方相加,右邊的懲罰項就也會越大,就很難最小化,藉此來控制特徵的使用量不可以太多
- 公式
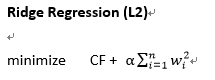
小補充:大家在網路上或書上,可能會看到損失函數(Loss Function)這個詞,然後可能會納悶說我這篇怎麼沒有提到,所以這邊要特別跟大家報告一下,我這篇使用的成本函數(Cost Function)等同於損失函數(Loss Function)喔
更詳細的迴歸模型教學與介紹,可以參考Sckit-Learn的官網(https://scikit-learn.org/stable/modules/linear_model.html#)喔
Reference
https://pyecontech.com/2019/12/28/python-實作-迴歸模型/
https://sckit-learn.org/stable/modules/linear_model.html#
https://yltang.net/tutorial/dsml/13/
https://kknews.cc/zh-tw/tech/4kkoqog.html
https://www.itread01.com/content/1546306589.html
https://ithelp.ithome.com.tw/articles/10187739