Machine Learning - 給自己的機器學習筆記 - Logistic Regression - 邏輯迴歸 - 二元分類問題 - Scikit-Learn - Sklearn 實作教學
哈囉哈囉,這篇是延續上一篇(Machine Learning - 給自己的機器學習筆 - Logistic Regression邏輯迴歸 - 二元分類問題 - 原理詳細介紹)的喔,所以就不會針對邏輯迴歸的原理多做介紹囉,會直接進入Sklearn的實作教學喔

數據集介紹
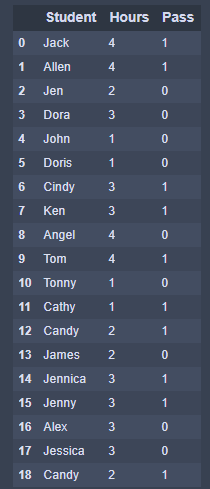
這邊有一組我自行捏造的數據集 ,說明了學生花在小考上的讀書時間(單位:小時)和最終是否有通過考試的數據,這個csv檔我會放在Github裡面喔,大家可以自行下載使用
參數
- penalty ({'l1', 'l2', 'elasticnet', 'none'}, default = 'l2'): 設定懲罰項的規範。'newton-cg'、'sag'和'lbfgs'求解器(solver)僅支持l2懲罰選項,'elasticnet'僅由'sag'求解器支援,如果設為none(liblinear 求解器不支援)助,代表不應用任何正規化
- dual (bool, default = False): 對偶或原始配方。對偶公式僅針對使用'liblinear'求解器的l2懲罰實現。當n_samples > n_features時,dual通常設定為False
- tol (float, default = 1e-4): 停止標準的公差,其實就是求解到多少的時候會停止,因為認定已經算出最佳解
- C (float, default = 1.0): 正則強度的倒數,也就是指正則係數λ的倒數
- fit_intercept (bool, defult = True): 指定是否應將常量(也稱為偏差或截距)添加到決策函數
- intercept_scaling (float, default = 1): 只有在使用求解器"liblinear",並將會fit_intercept設置為True時才有用,在這種狀況下,x變為[x,self.intercept_scaling],即為將常量值等於intercept_scaling的"synthetic(合成)"特徵附加到實例矢量。截距轉變為 intercept_scaling X Composite_feature_weight
注意! 和所有特徵一樣,合成特徵權重也要經過 l1 / l2 正規化。為了減輕正規化對合成權重(和對截距)的影響,必須增加intercept_scaling
- class_weight (dict or 'balanced', defualt = None): 與類相關的權重(格式: {class_label : weight}),用於標示分類模型中各種類型的權重,預設為不給值(None),代表不考慮權重,舉例: 如果對於二元模型,我們定義class_weight = {0: 0.9, 1 : 0.1},表示0的權重為90%,而1的權重為10%
如果設定為"balanced",會根據訓練樣本量來計算權重值,當某個樣本數量較多時,權重就會設低,反之樣本數量少,則權重會設比較高,計算權重公式: n_samples / (n_classes * np.bincount(y)),n_samples樣本數量,n_classes則為類別數量,np.bincount(y)會輸出每個類別的樣本數量視力,像是 y = [1, 0, 1, 0, 0, 1, 1],np.bincount(y) = [4, 3]
補充: class_weight 要用在什麼時候補?
分類模型中,我們會遇到的二元分類問題:
- 第一種 : 分類失誤的代價很高,像是對合格與不合格的食品來進行分類,誤將不合格的食品分類為合格的食品代價很高,寧可將合格的食品誤分類成不合格的食品,這時候可以使用人工甄選,但是卻不願將不合格的商品分類為合格的商品,此時可以提高不合格食品的權重
- 第二種 : 樣本比例嚴重失衡量,像是有合格與不合格的食品共一千箱,但是合格的有998箱,不合格的有2箱子,在不考慮權重的情況下班,可以把所有的測試集都預測為合格的食品,這樣準確率有99.8%,但是這樣一點意義也沒有,這個時候可以選擇"balanced",讓類庫自動提高不合格食品的權重
提高某個類別的權重,相較於不考慮權重,會有更多樣本被歸類到高權重的類別,這樣就可以解決上面兩種二元分類的問題
- random_state (int, RandomState instance, default = None): 隨機種子,但僅在求解器(solver)是 "sag"、"saga"或"liblinear"時有用
- solver ({'newton-cg', 'lbfgs' , 'liblinear', 'sag' ,'saga'}, default = 'lbfgs'): 選擇優化問題的算法,solver的選擇決定了對邏輯迴歸損失函數的優化方法,有以下四種選擇:
- liblinear: 使用坐標軸下降法來迭代優化損失函數(使用liblinear開源庫)
- lbfgs: 為預設選項,使用損失函數的二階導數矩陣(也就是海森矩陣)來迭代優化損失函數,類似於牛頓法
- newton-cg: 牛頓法的一種,一樣也是使用損失函數的二階導數矩陣(也就是海森矩陣)來迭代優化損失函數
- sag: 使用隨機梯度下降(為梯度下降的變種),它和一般的梯度下降法不同在於它每次迭代只用一部分的樣本來計算梯度,適合用於當數據樣本多的時候
- saga: 是線性收斂隨機優化算法的變種
補充: solver 如何選擇呢?
- 對於小型數據集,"liblinear"是一個不錯的選擇,而對於大型的數據集而言,"sag"和"saga"則更快
- 對於多類問題,只有'newton-cg'、'sag'、'saga'和'lbfgs'能處理多項式損失;'liblinear'受限於"one-versus-rest schemes",也就是使用'liblinear'的時候,如果遇到多分類問題的時候,會先把一種類別當成一個類別,然後其他所有類別當成另一個類別,以此類推,遍歷所有類別後,才進行分類處理
- 選擇'newton-cg'、'sag'、'lbfgs'這三種算法時,都需要有損失函數的一階或二階連續導數,所以不能夠用於沒有連續導數的L1正則化,只適用於L2正則化,而'liblinear'、'saga'則是兩者L1與L2都能使用
- 'saga'也支援penalty = 'elasticnet'
- 當penalty = 'none'的時候,'liblinear'是不可以使用的
補充: 如果不是大型數據集,為什麼不乾脆都用"liblinear"就好
'newton-cg'、'lbfgs'、'sag' 限制特別多,如果不是大型數據集,就都用 "liblinear" 不就好了?
對於多元邏輯迴歸,有 one-vs-rest(OvR) 和 many-vs-many(MvM) 兩種方法,MvM相較於OvR比較精準,但 "liblinear" 只支援OvR,這樣如果我們想要精準一點的多元迴歸模型就不能使用 "liblinear" 了喔,也就是說如果我們想要精確一點的多元迴歸模型就不能使用 L1 正則化囉
- max_iter (int, default = 100): 求解器(solver)收斂所需的最大迭代次數
- multi_class ({'auto', 'ovr', 'multinomial'}, default = 'auto'): 選擇分類方式,'ovr'就是one-vs-rest(OvR),而'multinomial'就是many-vs-many(MvM),當在處理二元邏輯迴歸問題時,'ovr' 和 'multinomial' 沒有差別,主要還是差在處理多元邏輯迴歸分類問題時
補充: one-vs-rest(OvR) 和 many-vs-many(MvM) 是什麼?
- one-vs-rest(OvR): 無論是多元邏輯迴歸還是二元邏輯迴歸,在這裡都看成是二元邏輯迴歸,它的方法是,假設我們今天要處理對於第A類的分類預測問題,我們會把所有的A類樣本當成正例,除了它以外的類別都當成負例,接著執行二元邏輯迴歸,就會得到第A類的分類模型,要獲得其他類的模型也是依照這種方法來以此類推獲得
- many-vs-many(MvM): MvM複雜的多,以MvM的特例one-vs-one(OvO)為例,假設模型有A類,而我們每次在A類樣本中選擇兩類樣本出來,標記為A1與A2,將所有被標記為A1與A2的樣本個別放在一起,把A1當成正例,把A2當成負例,接著執行二元邏輯迴歸,來獲得模型參數,也就是我們需要做 A(A - 1)/2 次分類
- 結論: 一般的情況下,one-vs-rest(OvR)的分類效果較many-vs-many(MvM)來得差,但MvM相較精準但計算速度上沒有OvR來得快,如果使用OvR,則四種的損失函數優化方法都可以使用(liblinear、newton-cg、lbfgs、sag),但multinomial只能選擇newton-cg、lbfgs和sag
- verbose (int, default = 0): 設定一個正數代表日誌的冗長度,預設為0,代表不輸出訓練過程,1表示偶爾輸出結果,大於1,則表示每個子模型都需要輸出
- warm_start (bool, default = False): 設定熱啟動,預設為False,當為True的時候,下一次訓練會重新使用上一次調用的解決方法當初始化方法
- n_jobs (int, default = None): CPU內核數,預設為1,代表使用一個核來執行程式,2代表兩個核執行,-1表示使用所有內核來執行
n_jobs 補充說明
如果multi_class = 'ovr',則在對類進行並行化時所使用的CPU內核數量,當求解器(solver)設定為'liblinear'時,無論是否指定了"multi_class",都會直接忽略此參數。除非在joblib.parrallel_backend上下文中,否則None表示1,-1表示使用所有的處理器來執行
- l1_ratio (float, default = None): 用來設定 Elastic-Net 的混合參數,0 <= l1_ratio <= 1。僅當penalty = 'elasticnet'時才能使用,設定為l1_ratio = 0等效於使用penalty = 'l2',而設置為l1_ratio = 1等效於penalty = 'l1',而當值介於0~1之間(0 < l1_ratio < 1),penalty則是L1與L2的組合
屬性方法
- classes_ (ndarray of shape (n_classes, )): 分類器已知的類別標籤列表
- coef_ (ndarray of shape (1, n_features) or (n_classes, n_features)): 決策函數中的係數值
- intercept_ (ndarray of shape (1, ) or (n_classes, )): 求截距(常量)
- n_iter_ (ndarray of shape (n_classes, ) or (1, )): 所有類別的實際迭代次數
詳細資訊,可以參考官網連結(https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html#sklearn.linear_model.LogisticRegression)
實作 1 - 二元分類問題
Step 1: 導入所需的套件
## 導入Python的數據處理套件 import numpy as np import pandas as pd ## 導入視覺化套件 import matplotlib.pyplot as plt ## 導入Sklearn中的線性模組 from sklearn import linear_model ## 將數據集分成訓練集與測試集的套件 from sklearn.model_selection import train_test_split
Step 2: 導入數據集
## 導入數據集
data = pd.read_csv('logistic_regression_sample.csv')
## 顯示數據集
data
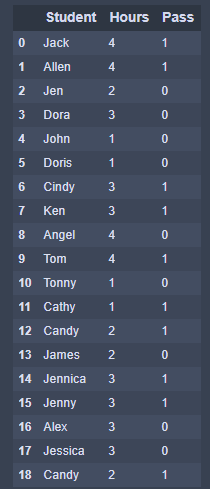
Step 3: 定義自變量與應變量
## 定義自變量與應變量
X = data['Hours'].values
y = data['Pass'].values
print('Independent Variable: ', X)
print('Dependent Variable: ', y)
Independent Variable: [4 4 2 3 1 1 3 3 4 4 1 1 2 2 3 3 3 3 2] Dependent Variable: [1 1 0 0 0 0 1 1 0 1 0 1 1 0 1 1 0 0 1]
Step 4: 將特徵向量轉為2D向量
- 由於 Sklearn 能接受的特徵格式為 (n_samples, n_features),所以使用 reshape 將特徵資料轉為2D向量,這樣 Sklearn 才能使用,一般狀況下,一維特徵才需要轉換
## 由於 Sklearn 能接受的特徵格式為 (n_samples, n_features),所以使用 reshape 將特徵資料轉為2D向量,這樣 Sklearn 才能使用,一般狀況下,一維特徵才需要轉換
print('Original X shape: ', X.shape)
## reshape用法: -1代表自動配置幾個框框(程式會自行根據有幾個值配置幾個框框架,也就是拿總共的數量除以後面設定框框內有幾個值)
## 轉為2D向量
X = X.reshape(-1, 1)
print(X)
print('After reshaping data to 2D vector : ', X.shape)
Original X shape: (19,) [[4] [4] [2] [3] [1] [1] [3] [3] [4] [4] [1] [1] [2] [2] [3] [3] [3] [3] [2]] After reshaping data to 2D vector : (19, 1)
Step 5: 將數據集分成訓練集與測試集
## 將數據集分成訓練集與測試集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
Step 6: 建立邏輯迴歸模型 Logistic Regression Model 與訓練模型
## 建立邏輯迴歸模型 model = linear_model.LogisticRegression() ## 擬和數據 model.fit(X_train, y_train)
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True, intercept_scaling=1, l1_ratio=None, max_iter=100, multi_class='auto', n_jobs=None, penalty='l2', random_state=None, solver='lbfgs', tol=0.0001, verbose=0, warm_start=False)
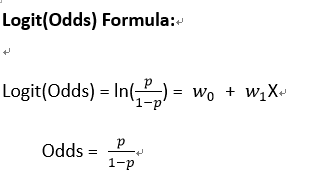
Step 7: 檢視模型係數與截距 Coeficient & Interception
## 查看建出來的模型係數與截距 y = w1x + w0
w1 = float(model.coef_)
w0 = float(model.intercept_)
print('Coeficient: ', w1)
print('Interception: ', w0)
Coeficient: 0.5672535305693119 Interception: -1.3328997193245475
Step 8: Sigmoid - 套入轉換函數 (將Logit(Odds)值轉換成 -> 0~1之間的數值)
## 套用 Sigmoid轉換函數,將值轉換成介於0~1 之間的值(機率) def sigmoid(x, w0, w1): logit_odds = w0 + w1 * x return 1 / (1 + np.exp(-logit_odds))
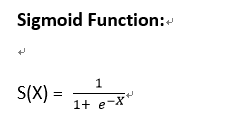
由於我們數據集這邊只有一個自變量來預測它的應變量,所以使用的是簡單線性迴歸公式來建模型 y = w0 + w1x
Step 9: 視覺化轉換結果圖
## 視覺化後Sigmoid圖 x = np.arange(0, 20, 1) result = sigmoid(x, w0, w1) plt.plot(x, result) ## 畫出50%的機率線 plt.axhline(y = 0.5, ls = 'dotted', color = 'y')
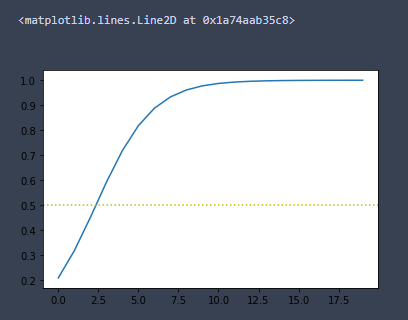
從圖中可以看出只要讀書時間超過2.5小時,就超過了50%的機率線,也就是邏輯迴歸會預測為及格Pass
Step 10: 預測測試集
## 預測測試集
prediction = model.predict(X_test)
print('Real Result: ', y_test)
print('Model Predict: ', prediction)
## 預測自行定義的數據集
result = model.predict([[1], [2], [2.5], [3], [3.5], [4], [5], [6]])
print('Define your own data and predict: ', result)
Real Result: [0 1 0 1] Model Predict: [1 1 0 0] Define your own data and predict: [0 0 1 1 1 1 1 1]
Step 11: 模型預測測試集中每筆數據為0或1的機率
## 預測測試集為1或0的機率
proba = model.predict_proba(X_test)
print('Probability (0 or 1)', proba)
Probability (0 or 1) [[0.4088163 0.5911837 ] [0.4088163 0.5911837 ] [0.54943612 0.45056388] [0.54943612 0.45056388]]
Step 12: 模型表現 - 準確度 Accuracy
## 模型表現
score = model.score(X_test, y_test)
print('Accuracy :' + str(score * 100) + '%')
Accuracy :50.0%
實作 2 - 多元分類問題
Step 1: 導入所需的套件
- 由於我們這邊要使用Sklearn中的內建數據集 - 鳶尾花數據集(Iris dataset),所以我們需要多導入一個datasets套件
## 導入Python的數據處理套件 import numpy as np import pandas as pd ## 導入視覺化套件 import matplotlib.pyplot as plt ## 導入Sklearn中的線性模組 from sklearn import linear_model ## 導入Sklearn的內建數據集 from sklearn import datasets ## 將數據集分成訓練集與測試集的套件 from sklearn.model_selection import train_test_split
Step 2: 導入數據集
- 相信大家都對大名鼎鼎的鳶尾花數據集並不陌生,這邊要展示的是處理多元分類問題,而鳶尾花數據集裡剛好將花分成三種類別,所以很適合拿它來DEMO
## 導入iris數據集(鳶尾花數據集) iris_data = datasets.load_iris() ## 顯示數據集 print(iris_data)
Step 3: 定義自變量與應變量
- 自變量: 特徵有四種
- 應變量: 共分成三類
## 定義自變量與應變量
X = iris_data.data
y = iris_data.target
print('Independent Variable: ', X)
print('Dependent Variable: ', y)
Independent Variable: [[5.1 3.5 1.4 0.2] [4.9 3. 1.4 0.2] [4.7 3.2 1.3 0.2] [4.6 3.1 1.5 0.2] [5. 3.6 1.4 0.2] [5.4 3.9 1.7 0.4] [4.6 3.4 1.4 0.3] [5. 3.4 1.5 0.2] [4.4 2.9 1.4 0.2] [4.9 3.1 1.5 0.1] [5.4 3.7 1.5 0.2] [4.8 3.4 1.6 0.2] [4.8 3. 1.4 0.1] [4.3 3. 1.1 0.1] [5.8 4. 1.2 0.2] [5.7 4.4 1.5 0.4] [5.4 3.9 1.3 0.4] [5.1 3.5 1.4 0.3] [5.7 3.8 1.7 0.3] [5.1 3.8 1.5 0.3] [5.4 3.4 1.7 0.2] [5.1 3.7 1.5 0.4]
Step 5: 將數據集分成訓練集與測試集
## 將數據集分成訓練集與測試集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
Step 6: 建立邏輯迴歸模型 Logistic Regression Model 與訓練模型
## 建立邏輯迴歸模型 model = linear_model.LogisticRegression() ## 擬和數據 model.fit(X_train, y_train)
Step 7: 預測測試集
## 預測測試集
prediction = model.predict(X_test)
print('Real y (test data): ', y_test)
print('Predict y (test data)', prediction)
## 查看模型預測0、1、2的機率
probability = model.predct_proba(X_test)
print('Probability (0 or 1 or 2): ', probability)
Real y (test data): [0 1 2 1 1 2 2 1 2 1 1 2 0 2 0 2 0 2 2 2 1 1 0 2 1 2 2 1 1 2] Predict y (test data) [0 1 2 1 1 2 2 1 2 1 2 2 0 2 0 2 0 2 2 2 1 1 0 2 1 2 1 1 1 2] Probability (0 or 1 or 2): [[9.63686532e-01 3.63132924e-02 1.75222019e-07] [1.07574506e-02 8.98088376e-01 9.11541730e-02] [2.49142162e-05 1.27485520e-01 8.72489566e-01] [2.35798020e-02 9.30301769e-01 4.61184292e-02] [2.19478761e-02 9.46475534e-01 3.15765897e-02] [1.43602535e-04 1.30353278e-01 8.69503120e-01] [1.11362279e-07 5.34629536e-03 9.94653593e-01] [1.03123468e-02 7.98148327e-01 1.91539326e-01] [5.56104282e-05 1.06288516e-01 8.93655874e-01] [3.15857582e-03 7.78516615e-01 2.18324809e-01] [7.69095917e-04 4.55551926e-01 5.43678978e-01] [2.36721813e-05 2.99622625e-02 9.70014065e-01] [9.80272061e-01 1.97278939e-02 4.48886032e-08] [7.31795353e-04 2.97582532e-01 7.01685672e-01] [9.73794169e-01 2.62057313e-02 9.97324567e-08] [1.44802727e-03 4.78512696e-01 5.20039277e-01] [9.79315374e-01 2.06845311e-02 9.47643193e-08] [2.04774841e-05 5.14453109e-02 9.48534212e-01] [7.54948158e-06 1.88378930e-02 9.81154558e-01] [8.96436493e-05 7.67452806e-02 9.23165076e-01] [1.09059868e-02 9.17394806e-01 7.16992073e-02] [1.88977619e-02 9.33269622e-01 4.78326163e-02] [9.49038620e-01 5.09607872e-02 5.92959951e-07] [4.38823090e-06 2.96993680e-02 9.70296244e-01] [5.85053775e-03 8.15952293e-01 1.78197169e-01] [4.09752857e-04 2.23191236e-01 7.76399012e-01] [7.61732149e-03 6.37508336e-01 3.54874343e-01] [2.50183895e-03 7.75078871e-01 2.22419290e-01] [1.34214049e-01 8.62185634e-01 3.60031710e-03] [1.09755114e-06 1.65768773e-02 9.83422025e-01]]
Step 8: 模型表現 - 準確度 Accuracy
## 模型預測訓練集的準確度
accuracy_train = model.score(X_train, y_train)
print('Accuracy (Train Data): ' + str(accuracy_train * 100) + '%')
## 模型預測測試集的準確度
accuracy_test = model.score(X_test, y_test)
print('Accuracy (Test Data): ' + str(accuracy_test * 100) + '%')
Accuracy (Train Data): 99.16666666666667% Accuracy (Test Data): 93.33333333333333%
Step 9: 邏輯迴歸模型 Logistic Regression Model 的其他相關資訊
## 其他相關的模型資訊
## 模型類別
print('Classes: ', model.classes_)
## 所有類的迭代次數
print("Classes Iteration: ", model.n_iter_)
## 模型係數
print('Coeficient: ', model.coef_)
## 模型截距
print('Interception: ', model.intercept_)
Classes: [0 1 2] Classes Iteration: [100] Coeficient: [[-0.45486217 0.88917554 -2.36931595 -1.0320416 ] [ 0.32867869 -0.25690156 -0.13017246 -0.76389135] [ 0.12618348 -0.63227398 2.49948841 1.79593295]] Interception: [ 9.66611776 2.58710172 -12.25321948]
又學會了一個模型了!! 這樣大家手上又多了一個強大的武器,面對未來遇到的問題就能夠多一種解決方法了,面對著學不完的 AI 知識,我還在努力著,一點一滴的累積著