NumPy 的各種用法 - 讀書筆記 - Python Data Science Handbook - Python數據科學 - NumPy Array的屬性與操作(串聯與切割 - Concatenate、hstack、vstack、split...
Github連結

2.3章 NumPy數組的運算:公用函数 Computation on NumPy Arrays: Universal Functions
1. 為什麼NumPy的數組進行計算操作時是非常快的?
計算NumPy的數組可以是非常快,也可以是非常慢的,然而快的原因:
- 向量化的操作
- 都是透過 NumPy 的通用函式(ufuncs : Universal Functions)來實現的
2. 為什麼Python的預設實作(又名為CPython),對於一些操作執行效率非常低?
- 原因: 因語言本身的動態和解釋執行的持性有關
- 說明: 因為類型是具有彈性的,因此不能像C或是Fortran一樣能將操作序列編譯成效率高的機器碼來執行
- 解決方法
- PyPy: Python的JIT(Just-in-time)編譯實現
- Cython: 將Python程式碼轉換成可編譯的C程式碼
- Numba: 將Python的程式碼轉換成快速的LVM字節碼 (bytecode)
3. Python中慢的循環- The Slowness of Loops
- 一個表現相對慢(低效)的方式在於重復進行很多細微的操作,像是對一個數組中的所有元素都進行循環操作
- 舉例計算每個元素的倒數
import numpy as np np.random.seed(1) def compute_reciprocals(array): ## 建一個空的NumPy Array來裝最終的計算結果 result = np.empty(len(array)) for i in range(len(array)): result[i] = 1.0 / array[1] return result ## 創建一個隨機的NumPy Array new_array = np.random.randint(1, 10, size = 5) ## 計算倒數 compute_reciprocals(new_array)
執行結果
array([0.11111111, 0.11111111, 0.11111111, 0.11111111, 0.11111111])
上面的程式碼,由於資料量不夠多,所以感覺計算起來不會太久,但是如果今天有一很大的數據集如下,那就讓我們來測試看看它的效率吧
big_data_array = np.random.randint (1, 100, size = 10000000) ## 計時 %time compute_reciprocals(big_data_array)
執行結果
Wall time: 1min 1s array([0.01818182, 0.01818182, 0.01818182, ..., 0.01818182, 0.01818182, 0.01818182])
從結果發現計算速度相當地慢!
結論
- 上面執行了千萬次的操作並儲存結果就需要機秒,然而手機中的處理是用Giga-FLOPS來衡量(等同於每秒數十億次的操作),相較之下真的是非常優呼
- 這樣的瓶頸與操作本身沒關係,而是每次循環時CPython都需執行類型檢查和函數匹配,每次計算倒數時,Python會先宣告物件(object)類型和找尋正確的函數來使用
- 如果我們使用的是編譯型的程式語言,每次進行計算時,類型和執行的函數都已經確定好,所以時間會快非常多
4. UFuncs 介紹 - 向量化的操作
NumPy是如何提高數組的計算性能的?
- 向量化操作:對於許多類型的操作,NumPy為這種靜態的類型提供了方便且編譯好的接口(函數)
- 運作原理: 向量化操作可以簡單應用於數組上,它可以再應用到每個元素裡,向量化操作原理就是將循環的地方放到NumPy編譯好的那一層(compiled layer),從而提高執行速度
NumPy一個數組的循環計算
舉例: 比較一下過去用Python的方法與用NumPy的方法
print('Python Loop Method: ', compute_reciprocals(new_array))
print('NumPy ufuncs Method: ', 1.0/new_array)
執行結果
Python Loop Method: [0.11111111 0.11111111 0.11111111 0.11111111 0.11111111] NumPy ufuncs Method: [0.16666667 0.11111111 0.16666667 1. 1. ]
這邊使用NumPy的ufuncs來計算執行時間,時間與前面用Python的循環差非常非常多
## 對大的數據准行計算執行特間 %timeit (1.0/big_data_array)
執行結果
122 ms ± 9.26 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
NumPy在兩個數組問的計算
- 重點: ,NumPy向量化操作是透過ufuncs來實現的,主要的意義就是在NumPy 數組中快速地執行重復的操作
a = np.arange(9)
print('a: ', a)
b = np.arange(1,10)
print('b: ' , b)
print('a/b: ', a/b)
執行結果
a: [0 1 2 3 4 5 6 7 8] b: [1 2 3 4 5 6 7 8 9] a/b: [0. 0.5 0.66666667 0.75 0.8 0.83333333 0.85714286 0.875 0.88888889]
- Ufuncs極端彈性的,上面的例子是標量(scaler)和數組間的操作計算,而我們也可以在兩個數組間實現這樣的操作
NumPy的多維數組計算
我們將一個3x3數組中的元素,進行4的x(元素值)次方計算
x = np.arange(9).reshape(3, 3)
print('original:')
print (x)
print ('Compute: ')
print (4**x)
執行結果
original: [[0 1 2] [3 4 5] [6 7 8]] Compute: [[ 1 4 16] [ 64 256 1024] [ 4096 16384 65536]]
結論
- 透過ufuncs向量化的操作計算,幾乎都會比使用Python循環(Loop)更加地高效,所以以後如果我們遇到Python數組循環操作的問題,就可以替换成NumPy的ufuncs這種向量化操作
5. NumPy數組的運算
基本的運算- +、、x、/、%、**等等
- NumPy的ufuncs可以非常自然地被使用,它採用了Python原生的計算符號,像是標準的加法、減法、乘法、除法
x = np.arange (6)
print ("x = ", x)
print ("x + 8 = ", x + 8)
print ("x - 4 = ", x - 4)
print("x * 6 =", x * 6)
print ("x / 2 = ", x/2)
## 整除計算
print ("x // 2 = ", x//2)
執行結果
x = [0 1 2 3 4 5] x + 8 = [ 8 9 10 11 12 13] x - 4 = [-4 -3 -2 -1 0 1] x * 6 = [ 0 6 12 18 24 30] x / 2 = [0. 0.5 1. 1.5 2. 2.5] x // 2 = [0 0 1 1 2 2]
- 求複數、冪次和餘數
print ("-x = ", -x)
print ("x ** 2 ", x ** 2)
print ("x % 2 = ", x % 2)
執行結果
-x = [ 0 -1 -2 -3 -4 -5] x ** 2 [ 0 1 4 9 16 25] x % 2 = [0 1 0 1 0 1]
- 可以依需求將各種運算结合
-(x**4 + 2) * 6
執行結果
array([ -12, -18, -108, -498, -1548, -3762], dtype=int32)
- 上面應用的是NumPy中函數的簡化寫法,像是+號代表的是add函數的封裝
np.add(4, x)
執行結果
array([4, 5, 6, 7, 8, 9])
- 表中列出的是計算符號與其對應的ufuncs函數
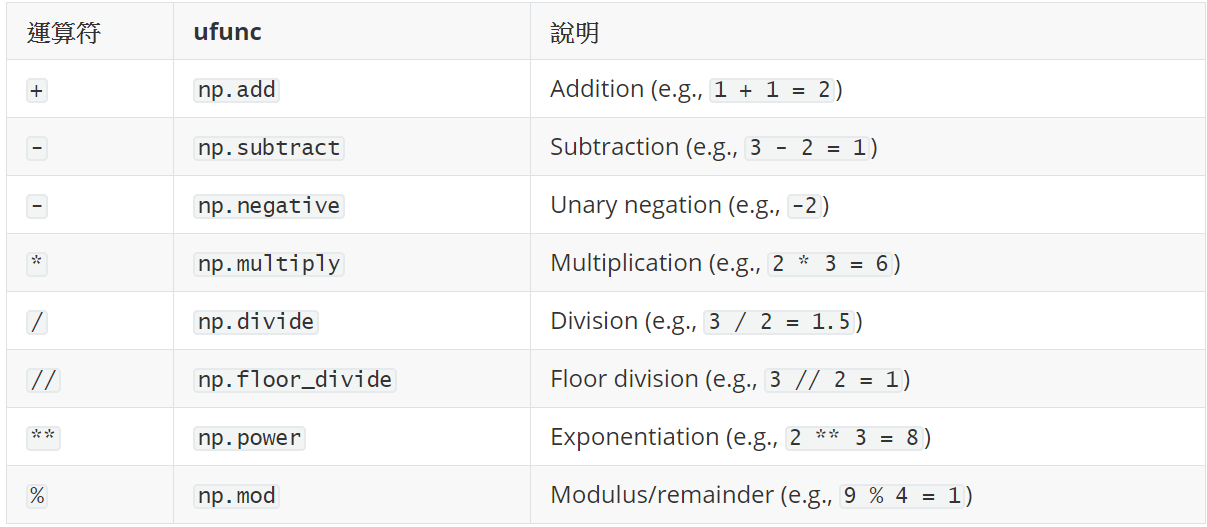
絕對值 Absolute Value
- Python内建的絕對值函數: 在NumPy中與算數一樣也能夠理解使用
x = np.array([-2,-6, -3,-7,-8,-6]) abs(x)
執行結果
array([2, 6, 3, 7, 8, 6])
- NumPy的ufuncs絕對值方法 - np.absolute、np.abs(,簡短的寫法)
print(np.absolute(x)) print(np.abs(x))
執行結果
[2 6 3 7 8 6] [2 6 3 7 8 6]
- ufuncs也可以處理複雜的數據(復數),返回的會是矢量的長度(大小)
## 要計算矢量長度的話一定要使用j x = np.array ([3 - 4j, 4 + 3j, 5 + 6j, 6 - 5j, 2 - 6j, 3 +7j]) np.abs (x)
執行結果
array([5. , 5. , 7.81024968, 7.81024968, 6.32455532, 7.61577311])
三角函數 Trigonometric Functions
- 定義一個角度的數組
theta = np.linspace(0, np.pi, 3)
- 計三角函數
print("theta = ", theta)
print ("sin(theta) = ", np.sin(theta))
print("cos(theta) = ", np.cos (theta))
print("tan(theta) = ", np.tan (theta))
執行結果
theta = [0. 1.57079633 3.14159265] sin(theta) = [0.0000000e+00 1.0000000e+00 1.2246468e-16] cos(theta) = [ 1.000000e+00 6.123234e-17 -1.000000e+00] tan(theta) = [ 0.00000000e+00 1.63312394e+16 -1.22464680e-16]
- 逆三角函數: 由於受到機器精確度(浮點數精度)的限制,结果中該為0的地方不等0,所以還提供了逆三角函數使用
x = [-1, 0 ,1]
print ("x = ", x)
print ("arcsin(x) = ", np.arcsin(x))
print("arccos(x) = ", np. arccos (x))
print ("arctan(x)= ", np.arctan (x))
執行結果
x = [-1, 0, 1] arcsin(x) = [-1.57079633 0. 1.57079633] arccos(x) = [3.14159265 1.57079633 0. ] arctan(x)= [-0.78539816 0. 0.78539816]
指數和對數 Exponents & Logarithms
- 指數計算
x = [0,1,2,3,4,5,6]
print("x = ", x)
print ("e^x = ", np.exp(x))
print ("2 ^ x =", np.exp2(x))
print ("3 ^ x = ", np.power(3, x))
執行結果
x = [0, 1, 2, 3, 4, 5, 6] e^x = [ 1. 2.71828183 7.3890561 20.08553692 54.59815003 148.4131591 403.42879349] 2 ^ x = [ 1. 2. 4. 8. 16. 32. 64.] 3 ^ x = [ 1 3 9 27 81 243 729]
- 對數函數: 指數的逆操作,np.log是自然對數算法,如果需要2的對數與10的對數算法,也有相對應的函數應用
x = [1,2,4,6,8,10]
print("x = ", x)
print ("In(x) = ", np.log(x))
print ("log2(x) = ", np.log2(x))
print ("log10(x) = ", np.log10(x))
執行結果
x = [1, 2, 4, 6, 8, 10] In(x) = [0. 0.69314718 1.38629436 1.79175947 2.07944154 2.30258509] log2(x) = [0. 1. 2. 2.5849625 3. 3.32192809] log10(x) = [0. 0.30103 0.60205999 0.77815125 0.90308999 1. ]
- 當輸人的值非常小時,可以保有精確度的指數和對數的函數方法
x = [0, 0.0001, 0.001, 0.00001, 0.1]
print ("exp(x) - 1 = ", np.expm1(x))
print ("log(1 + x) = ", np.log1p(x))
執行結果
exp(x) - 1 = [0.00000000e+00 1.00005000e-04 1.00050017e-03 1.00000500e-05 1.05170918e-01] log(1 + x) = [0.00000000e+00 9.99950003e-05 9.99500333e-04 9.99995000e-06 9.53101798e-02]
當輸入值很小時,這裡的函數會比np.log和no.exp計算的結果更加精確
6. 特殊的ufuncs Specialized ufuncs
- NumPy中當然還有更多的ufuncs,包括雙曲三角函式(hyperbolic trig functions),二進制位運算(bitwise arithmetic)
Scipy.special - 更多特別和晦澀的ufuncs
- 當我們需要使用一些特殊的數學函式來計算數據,scipy.special將會是我們可以尋找的選擇
- 舉例
from scipy import special
- Gama 函數 (廣義階層) 和相關數
## Gama 函數 (廣義階層) 和相關數
x = [1, 5, 10]
print ("gamma (x) = ", special.gamma (x))
print ("In|gamma x)| = ", special.gammaln(x))
print("beta(x, 4) = ", special.beta(x, 4))
執行結果
gamma (x) = [1.0000e+00 2.4000e+01 3.6288e+05] In|gamma x)| = [ 0. 3.17805383 12.80182748] beta(x, 4) = [0.25 0.00357143 0.00034965]
- 誤差函數(高斯積分)
## 誤差函數(高斯積分)
## 它的補數與反數
x = np.array([0, 0.2, 0.6, 0.8, 1.0])
print ("erf (x) = ", special.erf (x))
print ("erfc(x) = ", special.erfc(x))
print ("erfinv(x) = ", special.erfinv(x))
執行結果
erf (x) = [0. 0.22270259 0.60385609 0.74210096 0.84270079] erfc(x) = [1. 0.77729741 0.39614391 0.25789904 0.15729921] erfinv(x) = [0. 0.17914345 0.59511608 0.9061938 inf]
- 如果想要知道更多有關scipy.special與NumPy的資訊,可以在網路上搜尋"gamma function python"這個關鍵詞
7. 進階的Ufunc功能 Advanced Ufunc Features
out - 指定output
對於大型的計算,out這個方法非常有用,可以直接指定數組的計算结果會被放到哪個數組,而不是創建一個暫時的數值數組,這個方法可以直接將計算结果放到我們指定的內存位置
- 舉例: 創建一個1-5的數組x,與一個空的數組y,直接將x每個元素乘以10的结果指定放到y數組中
x = np.arange (10) print(x) y = np.empty(10) np.multiply(x, 10, out = y) print(y)
執行結果
[0 1 2 3 4 5 6 7 8 9] [ 0. 10. 20. 30. 40. 50. 60. 70. 80. 90.]
- 甚至可以使用之前提到的數組視圖一起使用
y = np.zeros(20) ## 在y數组中每隔一個位置播人一個2**x np.power(2, x, out = y[::2]) print (y)
執行結果
[ 1. 0. 2. 0. 4. 0. 8. 0. 16. 0. 32. 0. 64. 0. 128. 0. 256. 0. 512. 0.]
結論
如果我們换成這樣寫y[::2] = 3x,就會創建一個臨時數組來保存3 x结果,然後會執行第二次的操作,將結果複製到y數祖中,對於數據小的時候,感覺與ufunc沒有什麼太大區別,但數據量大時,謹慎使用out將會幫助我們省下大量的内存空間
聚合 Aggregates
- 對於二進制的ufuncs,可以直接從物件(object)中計算一些有趣的聚合
- 舉例來說,我們想要透過特定操作來縮小數組,則可以使用ufuncs的reduce方法
reduce
將指定操作重復應用於數組中,直到最後僅保留單個結果
- 舉例一: 我們想透過加法來縮減數組,它會將所有數組內的元素相加
x = np. arange (1, 10)
print ("x = ", x)
## 將x中每個元素相加, 縮减為一個值
np.add.reduce (x)
執行結果
x = [1 2 3 4 5 6 7 8 9] 45
- 舉例二: 透過乘法來縮減數組
np.multiply.reduce(x)
執行結果
362880
accumulate
會將特定操作每次對數組中的元素計算結果都印出,也就是保留中間過程的計算
- 累加的邊程
## 累加的邊程 np.add.accumulate(x)
執行結果
array([ 1, 3, 6, 10, 15, 21, 28, 36, 45], dtype=int32)
- 累乘的過程
## 累乘的過程 np.multiply.accumulate(x)
執行結果
array([ 1, 2, 6, 24, 120, 720, 5040, 40320, 362880], dtype=int32)
Outer products - 允許有兩個輸入源
- 說明任何的ufunc都可以使用外部方法來計算兩個不同的輸入源,並導出結果
- 應用舉例: 可以只用一行来創建一個乘法表等等
x = np.arange(1,10) ## 99乘法表 np.multiply.outer(x, x)
執行結果
array([[ 1, 2, 3, 4, 5, 6, 7, 8, 9], [ 2, 4, 6, 8, 10, 12, 14, 16, 18], [ 3, 6, 9, 12, 15, 18, 21, 24, 27], [ 4, 8, 12, 16, 20, 24, 28, 32, 36], [ 5, 10, 15, 20, 25, 30, 35, 40, 45], [ 6, 12, 18, 24, 30, 36, 42, 48, 54], [ 7, 14, 21, 28, 35, 42, 49, 56, 63], [ 8, 16, 24, 32, 40, 48, 56, 64, 72], [ 9, 18, 27, 36, 45, 54, 63, 72, 81]])