LeetCode學習筆記 - Binary Tree 二元樹 - 觀念介紹
Github連結

1. 樹的基本介紹
- 為一種抽象的資料類型(ADT)或是實作這一種抽象資料類型的資料結構,用來描述具有樹狀結構性質的資料結構
- 樹的節點個數為一或多個有限的集合,且必須存在一個根節點,根節點會分枝成n個不會交集的子節點,而這些子節點各自都為一個子集合,而一個子集合也為一顆子樹
名詞介紹
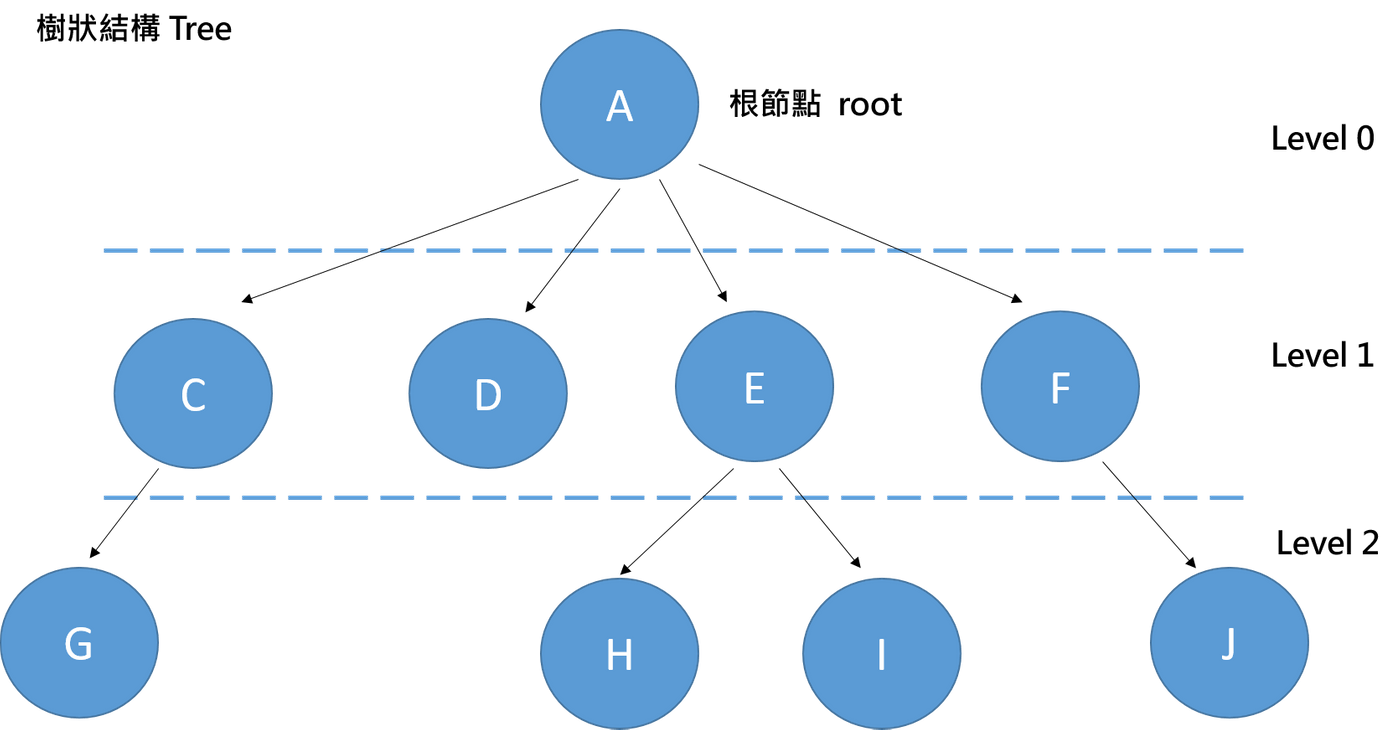
- 根節點(Root): 第一個節點,它不具有復節點,像是圖中的節點A
- 葉節點(Leaf): 此節點已經是最後的分支了,不再具有子節點,像是圖中的G、D、H、I、J
- 祖先節點(Ancenstors): 指某個節點到根節點之間所經過的所有節點,都為這個節點的祖先節點
- n元樹; 表示這個樹的節點最多有n個分支子節點
- 分支度(Degree): 美個節點分支的子節點數量,像是E的分支度為2
- 階層(Level): 由根節點開始計算,隨著子節點不斷往下計算階層數,如果右側的階層樹
- 樹高(Height): 又稱為深度(Depth),表示為此樹的最大階層樹,像圖中的樹高就是3
- 非終端節點(Noterminal Nodes): 只要還有子節點就算非終端節點
2. 什麼是BInary Tree?
- 二元樹指的就是每個節點最多只有兩個分支(也就是子節點樹量只會有小於兩個)的樹狀結構,由根節點分支成左右子樹(稱為左子樹和右子樹),且其分支具有左右順序不能顛倒
- 二元樹用在資料結構上,通常會是對節點定義一個標記函式,將一些值和每個節點建立相關聯,這樣標記的二元樹就能夠實現二元搜尋樹和二元堆積,目的是可以應用於高效率的搜尋和排序
實用算法
- 二元樹中的第i層,最多可以具有2的i - 1次方個節點數量
- 樹高度為k的二元樹,最多可以擁有2的k+1次方減1的節點數量,而節點數量與此公式結果計算出來的相等,稱為完滿二元樹
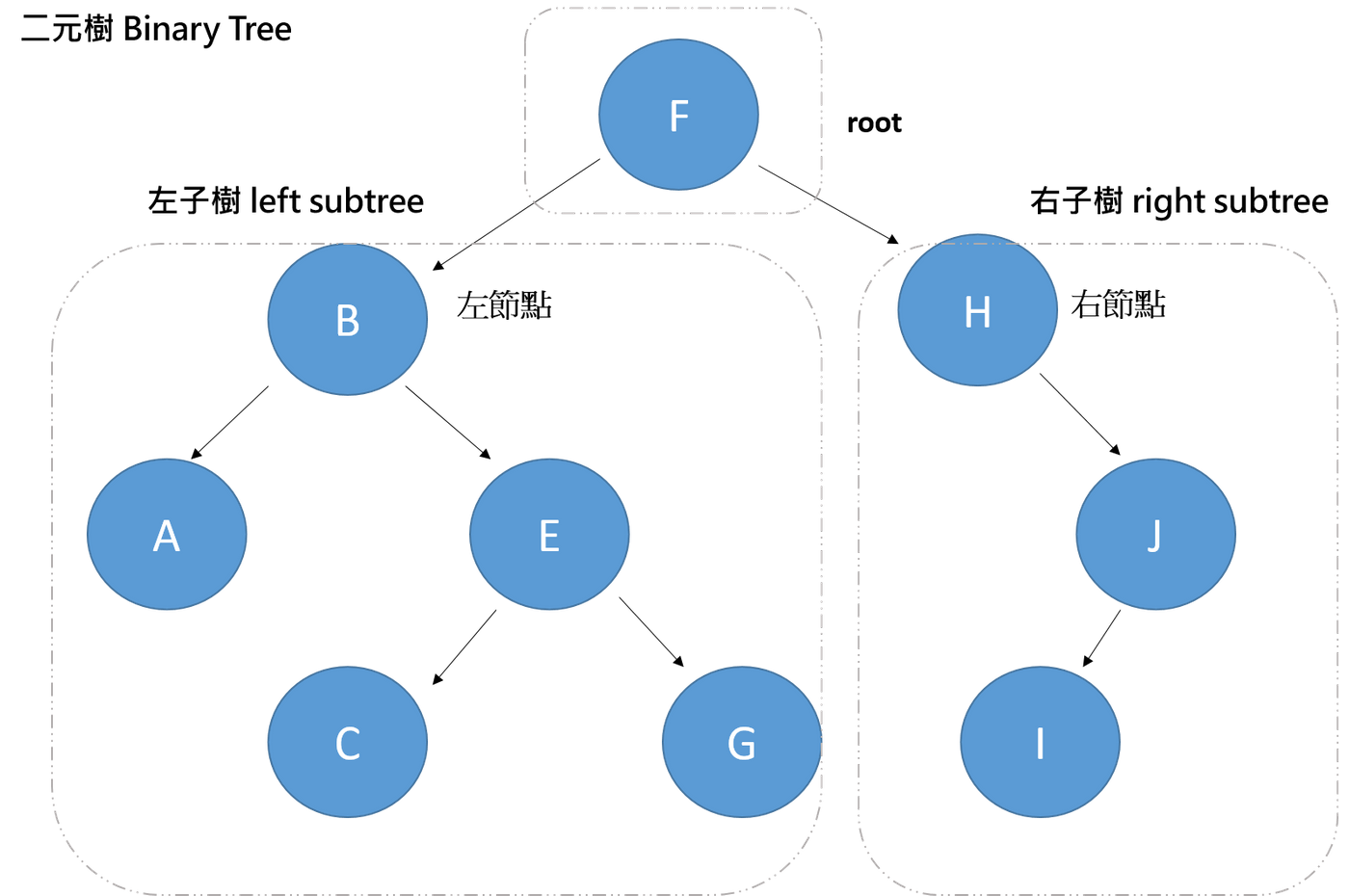
提醒: 當節點並沒有左右兩邊的都具有節點,沒有的那一邊會連接到空節點NIL(None/null)
3. 二元樹種類 - 完滿二元樹、完整二元樹、歪斜樹
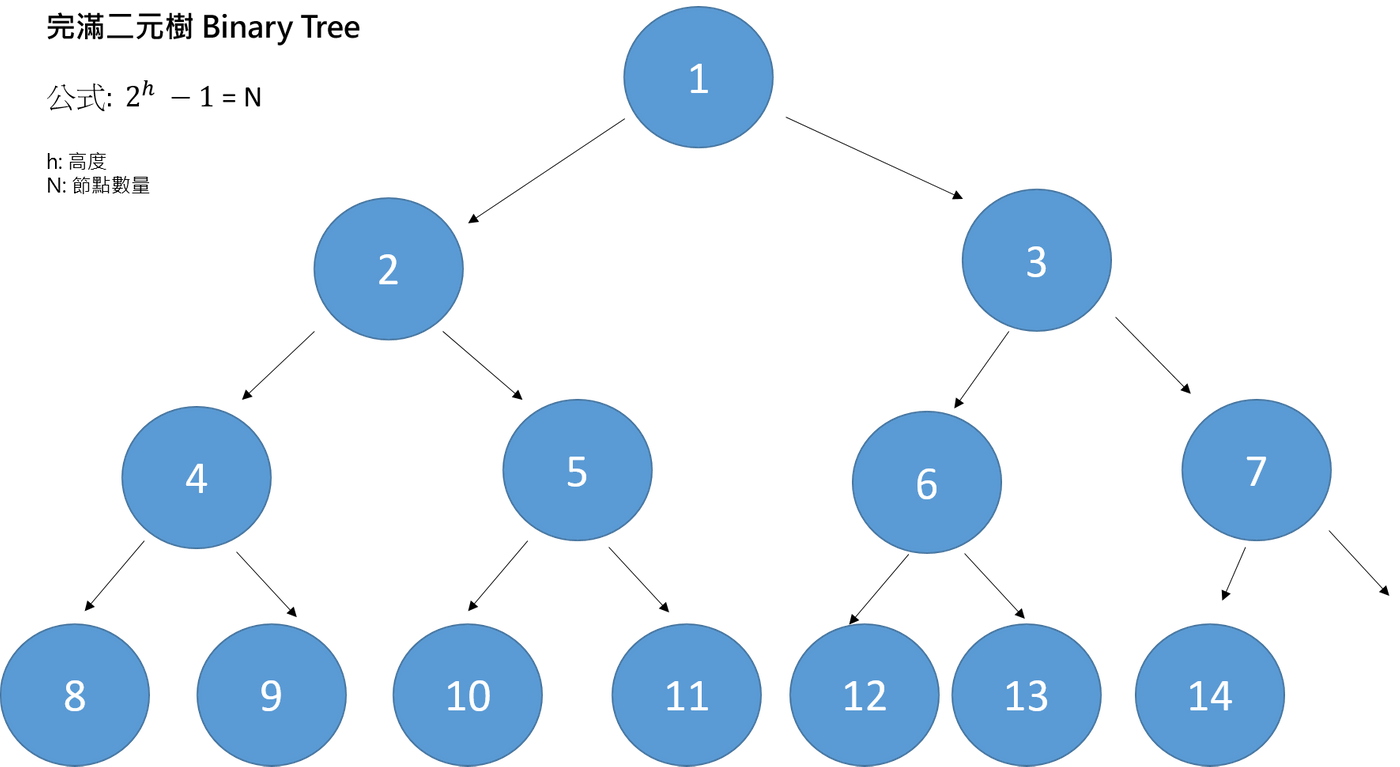
完滿二元樹 Fully Binary Tree
指的就是沒有任何一個節點會只有單獨連接的左或右節點,而計算節點數量就可以透過公式來達成

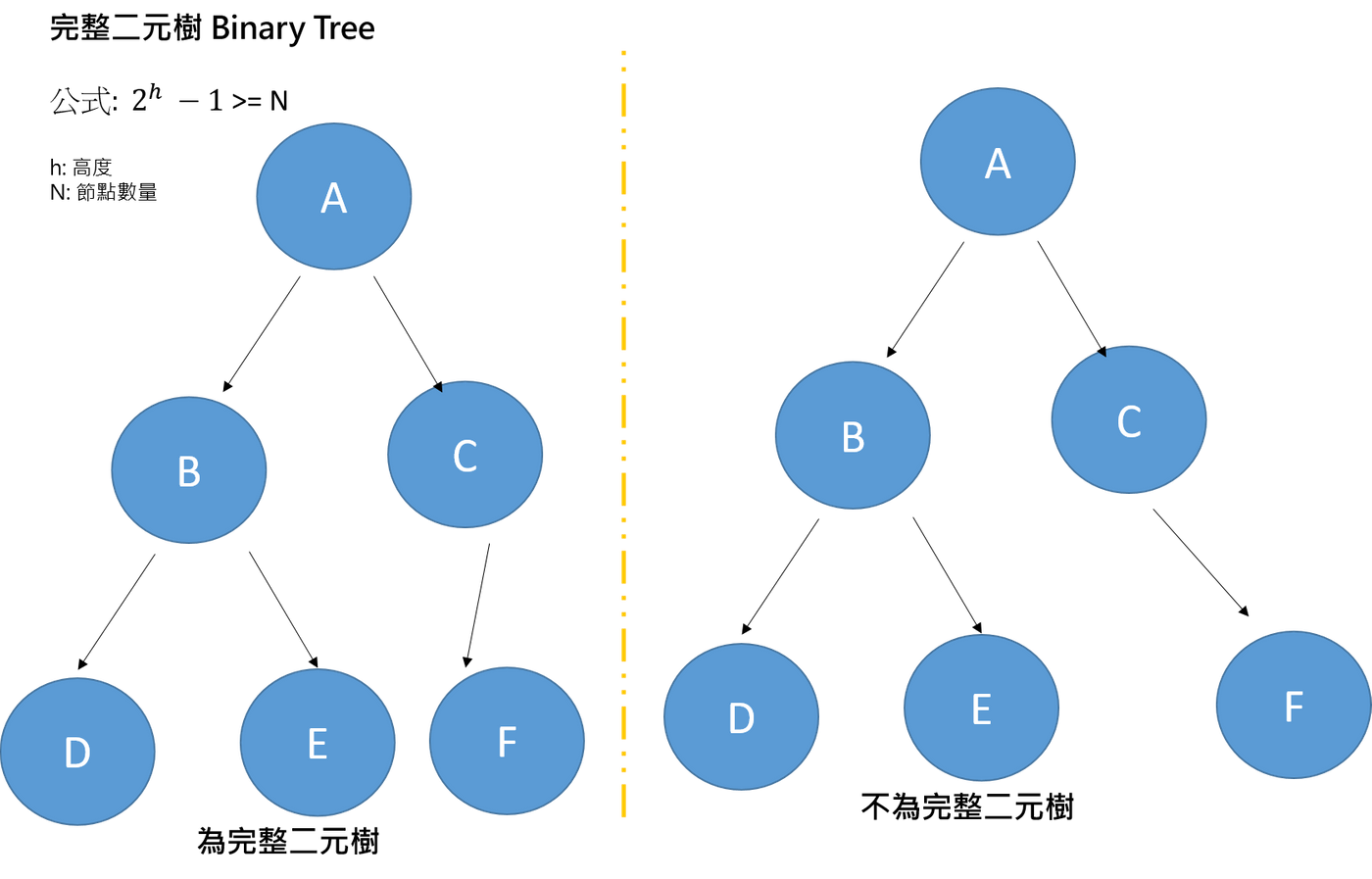
完整二元樹 Complete Binary Tree
如果高度為h,其節點的數量會小於等於公式

須符合從上到下,從左到右的規則,也就是可以只有左節點,但不能只有右節點
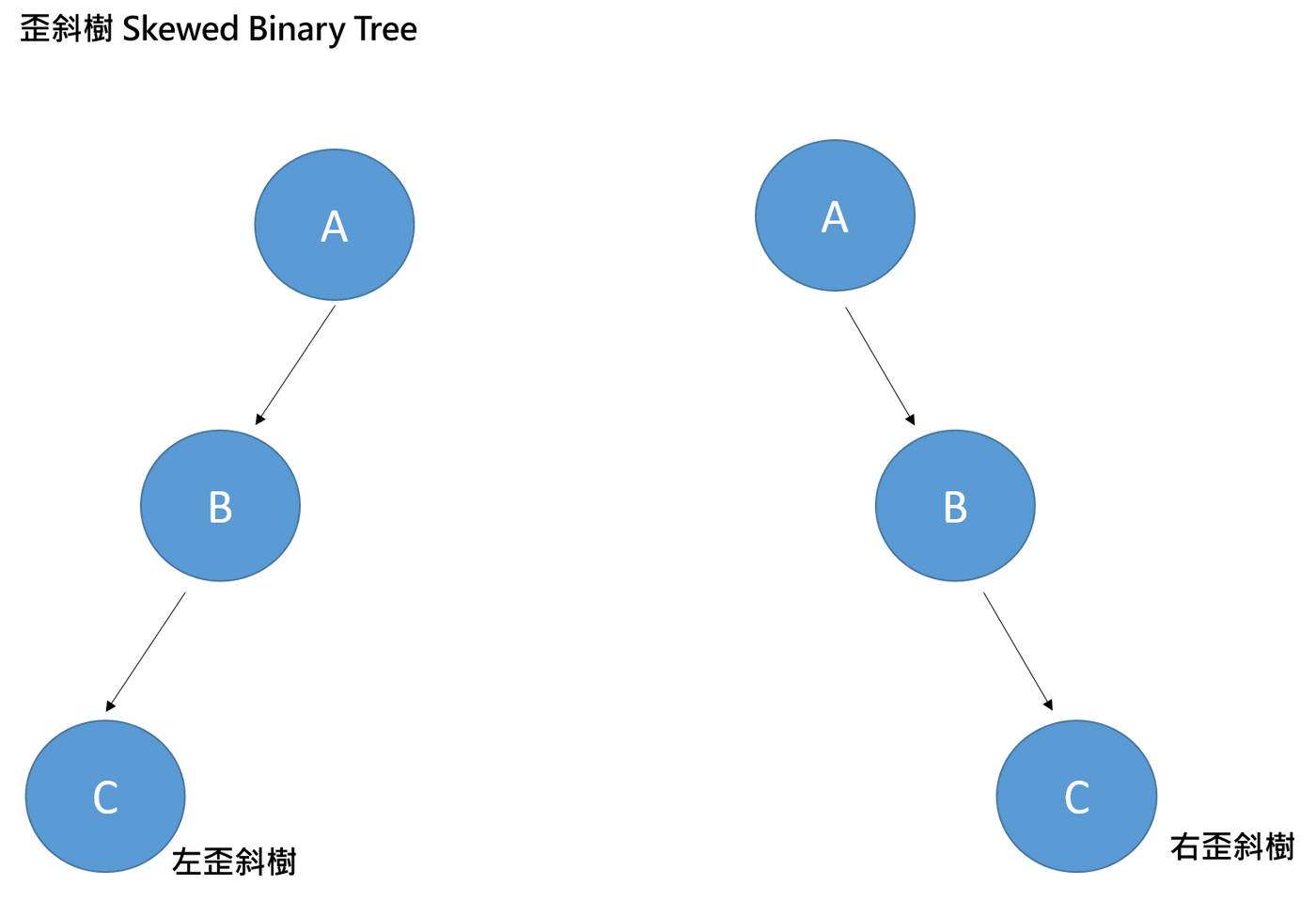
歪斜樹 Skewed Binary Tree
只有一邊的節點,只有左邊節點就為左歪斜樹,右邊就為右歪斜樹
4. 二元樹 適用範圍?
- 樹狀結構下分支最多只有兩個方向的時候(超過兩個方向: 字典樹,全部都只有一個方向: Linked List)
- 當為二元樹的前置狀況時
- 當我們不在乎節點值大小的關係時,也就是非二元搜尋樹的狀況
補充: 二元搜尋樹用在當我們需要快速在樹狀結構下搜尋某個節點的值,因為它規定右邊的節點會比自己小,左邊的節點會比自己大
Reference
https://zh.wikipedia.org/wiki/二叉树
https://zh.wikipedia.org/wiki/线索二叉树
http://wayne.cif.takming.edu.tw/datastru/tree.pdf