LeetCode學習筆記 - Dynamic Programming 方法 - LeetCode第62題 & 第63題 - 解法
Github連結

1. 62題
題目
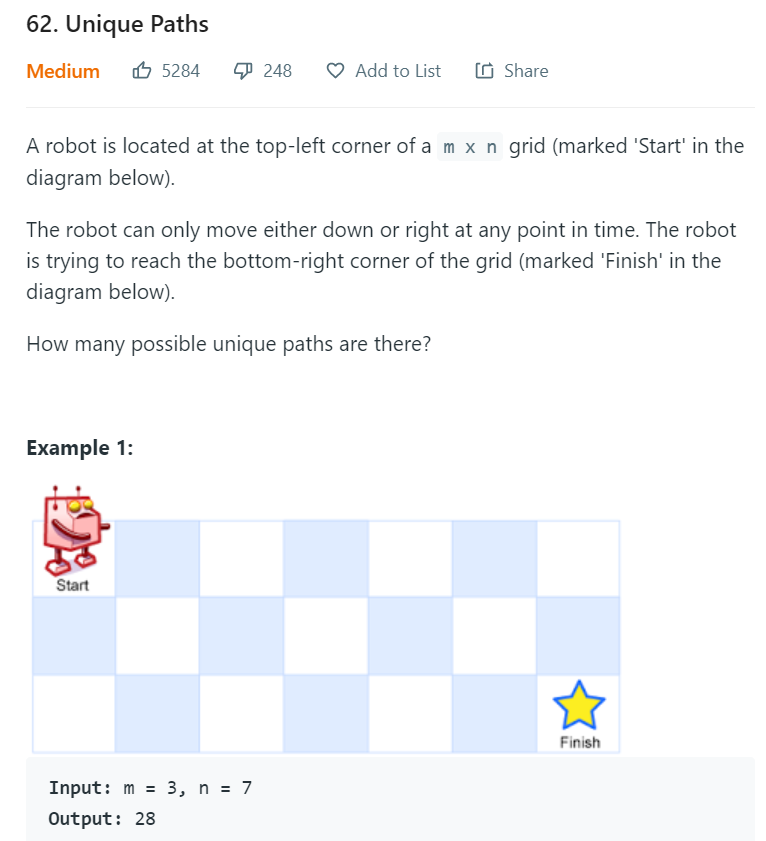
題目說明: 有一個機器人位於m x n 網格的左上角位置,機器人只能在同一個時間點進行向下或向右移動,而機器人的目標是到達網格的右下角位置,請問有多少種可能的唯一路徑?
解法
討論: 不重複的方法數量
- 過程中機器人沒辦法回頭,而且只能向右或向下走
- 走到目標的方法 = 走到目標上面一格的方法 + 走到目標左邊一格的方法,因為上面規定只能向右或向下,所以走到目標的前一步,一定是走到目標的上面或左邊
- 如果目標的上面一格或左邊一格已經超出了範圍(也就是碰到邊界),這樣無法走過來的位置,代表方法數為0
- 當目標就是起點(1x1的地圖),由起點開始走,這樣也算一種方法
解法:
- 創建一個二維串列dp
- 將dp最左邊跟上面的row/column設定為1,因為如果目標在邊界(左邊或上邊),只會有一種路徑可以到達
- 路徑由左至右,由上而下,並把當前位置設定為(i, j)
dp[i][j]=dp[i-1][j]+dp[i][j-1],也就是前面所討論的到達任何位置的方法,會是到達它左邊的方法加上到達它上面的方法- 執行迴圈計算,最後一格就會是我們的答案,回傳
dp[-1][-1]或是dp[m-1][n-1]
class Solution: def uniquePaths(self, m: int, n: int) -> int: ## 初始化二維串列: 創建一個都為0的二維串列 dp = [[0 for i in range(n)] for j in range(m)] ## 將最左邊和最上面設為1 for i in range(m): dp[i][0] = 1 for j in range(n): dp[0][j] = 1 ## 到達任何一個的方法為: 到達目標左邊一格的方法 + 到達其上面一格的方法 ## 設1~m跟1~n,那個1是因為如果目標就是起點,起點也算一種方法 for i in range(1, m): for j in range(1, n): dp[i][j] = dp[i-1][j] + dp[i][j-1] ## 回傳最後一個位置的值,即為目標的方法數 return dp[-1][-1]
2. 63題
題目
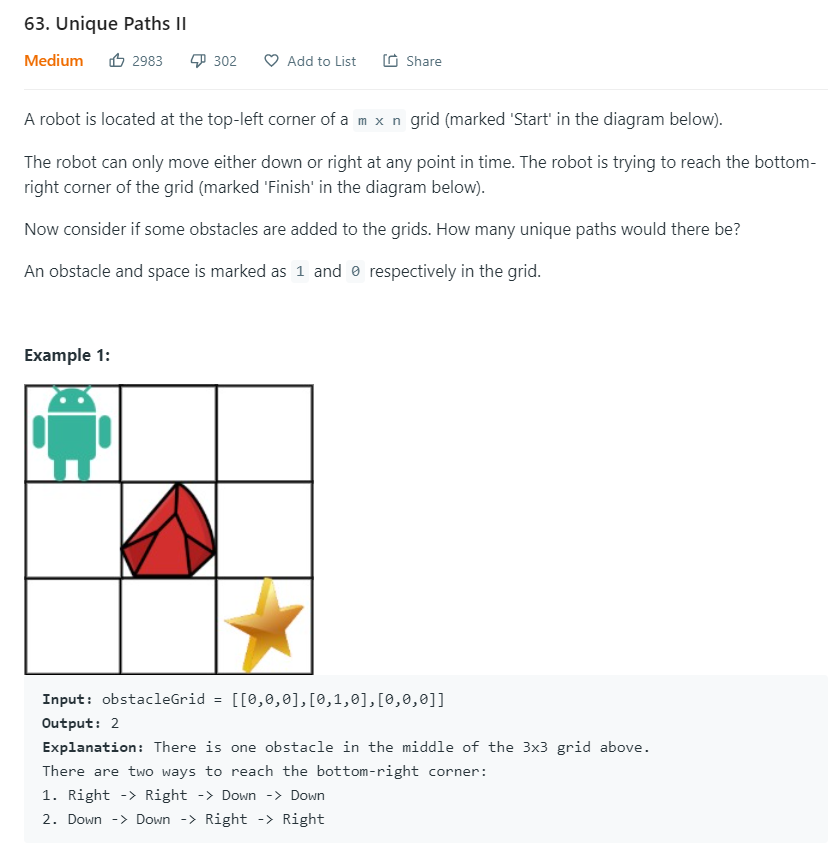
題目說明:
有一個機器人位於m x n網格的左上角位置,機器人只能在同一個時間向下或向右移動,機器人的目標是要走到右下角,如果中間出現了障礙物,那它到達目的地會有多少種唯一的路徑?障礙物會在網格中標記為1,一般空間則會標記為0
解法
討論
- 如果障礙物在(0, 0)的位置,就可以直接回傳0,因為被堵死了根本走不到
- 每次要進行計算前要先檢查當前的位置是否有被障礙物堵住
- 要特別留意邊界問題,i-1 >=0, j-1 >= 0,也就是要同時考慮目標的上面有沒有格子,左邊是否有格子
解法
- 創建一個二維串列dp
- 檢查網格(obstacleGrid)的起點位置是否有被障礙物堵住,有就直接回傳0
迴圈: 由左到右,由上到下,設定當前位置為(i, j),而且要檢查確定有障礙物(1)
- 如果沒有超過邊界的情況: 將
d[i][j]+d[i-1][j]&d[i][j-1] - 特別留意要分別檢查 i - 1 和 j -1 是否大於等於0,如果小於表示位於邊際,如果是在最左邊的邊際那我們只能加到達目標上面一格的方法數,如果是最上面就只能加到達目標左邊一格的方法數
迴圈執行結束後,最後一格就會是我們的答案,傳回dp[-1][-1]或是dp[m-1][n-1]
class Solution: def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int: ## 判斷網格是否為空,或是第一格被障礙物擋住,如果其中之一成立就回傳0 if obstacleGrid == None or obstacleGrid[0][0] == 1: return 0 ## 取得長寬 m, n = len(obstacleGrid), len(obstacleGrid[0]) ## 創建二維串列 dp = [n*[0] for s in range(m)] ## 到達起點也一是一種方法 dp[0][0] = 1 for i in range(m): for j in range(n): ## 當(i, j)這個位置沒有障礙物 if obstacleGrid[i][j] == 0: ## 當目標不是在最左邊,可以加上到達目標左邊那一格的方法數 if i-1>=0: dp[i][j] += dp[i-1][j] ## 當目標不是在最上面,可以加上到達目標上面那一格的方法數 if j-1 >= 0: dp[i][j] += dp[i][j-1] ## 回傳最後一格,即為結果 return dp[-1][-1]