AI金融科技應用實務 - Day1 課程筆記 - Python與金融 - Black-Scholes Model (BSM)觀念 - 實作蒙地卡羅估價演算法,來幫助我們推導出股票的合理價格 - Part2
Github連結

1. Python在金融業中所解決的問題
- 即時分析的需求不斷提高
- 對於數度、頻率和數據量需求的大幅提升
- 新拓展的業務和創新的動力需仰賴科技來推動
- 金融業所負擔的技術成本
2. Black-Scholes Model (BSM) 觀念 與 實作
老師想用Black-Scholes Model (BSM) 帶大家了解如何使用Python來實作演算法,這邊想用BSM數學模型,並使用蒙地卡羅估價演算法 Monte Carlo Method來實作
什麼是Black-Scholes Model (BSM)?
- 首先由美國經濟學家麥倫.舒爾斯和費雪.布萊克提出
- 為一種衍生性金融商品中的期權定價的數學模型
- 此模型適用於沒有派發股利的歐式期權
- 模型說明期權的潛在風險因素將會遵從幾何布朗運動(Geometric Brownian Motion)
補充: 羅伯特.C.墨頓在之後修改了模型,讓模型也可以針對派發股利的情況下使用
接下來我們將透過蒙地卡羅估價演算法 Monte Carlo Method來模擬針對歐式買權的估價,簡單來說就是我們使用Monte Carlo Method來推論出我們合理的買進股票價格
於Black-Scholes Model (BSM)模型中,到期日股價會由下面的公式推導出來的隨機變數
計算公式
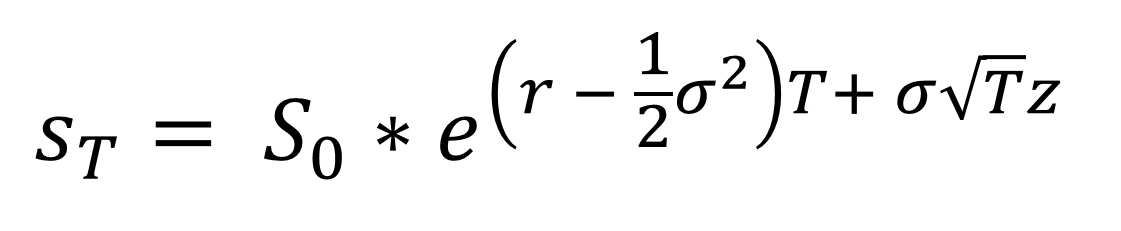
參數解釋
- 初始股價: S0
- 歐式買權履約價: K
- 到期日所剩時間(單位: 年): T
- 無風險利率: r
- 波動率: sigma
- 標準常態分佈的隨機變數(不需要自行設定): z
蒙地卡羅估價演算法 - 實作
什麼是蒙地卡羅估價演算法 Monte Carlo Method?
- 又稱為統計類比方法
- 為一種機率統計理論為指導的數值計算方式,指使用亂數(或是更加常用的偽亂數)來處理很多計算問題的方法
- 根據資產價格的變動進行一場隨機的模擬,進而推出選擇權的可能價格
計算過程
- 將從標準常態分佈中抽取I個偽隨機數值z(i),I也會代表我們將要使用Monte Carlo Method模擬幾次
- 針對每個給定z(i),推導出到期日的可能股價 ST: ST = S0 * np.exp((r - sigma ** 2 / 2) *T + sigma * math.sqrt(T) * z)
- 計算出所有到期日的選擇權內含價值(intrinsic value): hT = np.maximum(ST - K, 0)
- 使用Monte Carlo Method估計值來計算選擇權理論現值: C0 = math.exp(-r * T) * np.mean(hT)
import math
import numpy as np
S0 = 100 # 初始股價
K = 105 # 歐式買權履約價
T = 1.0 # 到期日所剩時間
r = 0.05 # 無風險利率
sigma = 0.2 # 波動率
I = 100000 # 模擬蒙地卡羅幾次
np.random.seed(1000) # 初始化偽隨機變數
z = np.random.standard_normal(I) # 抽取標準常態分佈隨機亂數
print(z)
ST = S0 * np.exp((r - sigma ** 2 / 2) *T + sigma * math.sqrt(T) * z) # 求算到期日股價
print(ST)
hT = np.maximum(ST - K, 0) # 求算到期日選擇權內含價值
print(hT)
C0 = math.exp(-r * T) * np.mean(hT) # 求算蒙地卡羅估計直
print('Value of the European call options = {:5.6f}.'.format(C0))
執行結果
[-0.8044583 0.32093155 -0.02548288 ... 2.05563421 -0.31621237 -0.19326188] [ 87.73128167 109.8764437 102.52161044 ... 155.44578614 96.73039856 99.13849486] [ 0. 4.8764437 0. ... 50.44578614 0. 0. ] Value of the European call options = 8.019103.
補充:本利和公式 - 實作
capital = 100 ## 本金 r = 0.05 ## 投資年限 T = 1 ## 期數 total = capital * (1 + r) ** T print(total)
執行結果
105.0
3. 為什麼Python適合當金融科技實作的語言?
從上面的實作中,我們可以知道為什麼使用Python來進行金融技術模型的實作是相當有用的
- 語法: Python的語法相當界進數學公式與法(像是帶入參數值時)
- 翻譯: 大部分的情況下,可以用一行Python程式碼來表達很多種的數學演算法
- 向量化: 使用NumPy很大的優點之一,就是簡潔的向量化語法撰寫(像是可以在一行程式碼中執行1000次的計算)
4. 課堂實作
情境: 針對標普500指數架構的資料,分析過往幾年的歷史指數價格,觀察指數的波動率是如何跟著時間波動的,並希望能夠證明波動率跟著時間變動而波動,而不是像一些典型的模型所假設的波動率為不變的常數
import numpy as np
import pandas as pd
from pylab import plt, mpl
## 視覺化的設定
plt.style.use('seaborn')
mpl.rcParams['font.family'] = 'serif'
%matplotlib inline
## 導入數據集
df = pd.read_csv('tr_eikon_eod_data.csv')
## 拿出'.SPX'數據,並組成DataFrame
data = pd.DataFrame(df['.SPX'])
## 將缺失值移除掉
data.dropna(inplace = True)
print(data.info())
## 用向量化方式進行Log運算,所計算出的值
data['rets'] = np.log(data / data.shift(1)) ## shift 將數據向下移動一位
## 計算推導出滾動的年化波動率
data['vola'] = data['rets'].rolling(252).std() * np.sqrt(252)
## 視覺化 - 指數價格、波動率
data[['.SPX', 'vola']].plot(subplots = True, figsize = (10, 6))
執行結果

Reference
https://zh.wikipedia.org/wiki/蒙地卡羅方法