小白刷刷刷 59 ～ 旋转的矩阵 2

基本信息

• 题号：59
• 题厂：微软
• 难度系数：中

---

解题思路

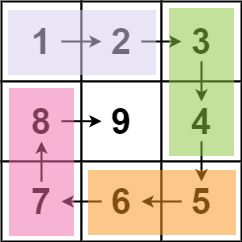
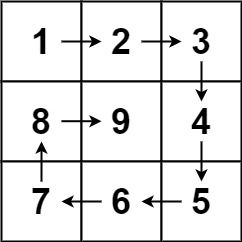
在 n * n 的正方形矩阵中按顺时针螺旋方式填入 1 ～ n^2

• 我们可以先创建一个 n * n 的空白矩阵，再按顺时针旋转思路对号填入数字。
• 每到拐点（左上，右上，左下，右下）四个角时，改变旋转方向。

---

class Solution:
  def generateMatrix(self, n: int) -> List[List[int]]:
       # 创建 n * n 空白矩阵
       matrix = [[0] * n for i in range(n)]
       # 上、下、左、右 边界
       t, b, l, r = 0, n - 1, 0, n - 1 
       
       # i 为填入数字，从 1 开始填
       i = 1
       # 当前行、列 index 号，从 [0][0] 开始填
       cur_r, cur_c = 0, 0
  
       while l <= r and t <= b:
           # 从左往右填，每填一次 i + 1，当前列往右移动一格，直到矩阵最右列跳出循环
           while cur_c < r and cur_r == t:
              matrix[cur_r][cur_c] = i
              i += 1
              cur_c += 1
           # 填完之后，top 边界 + 1，已备下次循环旋转时判断
           t += 1
    
           # 沿着最右边界，从上往下填。。。每一次行数 + 1 而列数不变
           while cur_r < b and cur_c == r:
              matrix[cur_r][cur_c] = i
              i += 1
              cur_r += 1   

           r -= 1

           # 重复以上步骤，沿着下边界从右往左填。。。 
           while cur_r == b and cur_c > l:
              matrix[cur_r][cur_c] = i
              i += 1
              cur_c -= 1
  
           b -= 1
  
           # 沿左边界，由下往上填   
           while cur_r > t and cur_c == l:
              matrix[cur_r][cur_c] = i
              i += 1
              cur_r -= 1

           l += 1

        # 不要忘了，跳出循环后，最后一个格子还没有填。。。
        matrix[cur_r][cur_c] = i   

        return matrix

---

Constraints

• 题目限制 1 <= n <= 20

考试时，向考官确认 n 的取值范围。

Big O

• Time：O（n^2）
• space：因为创建矩阵，自然复杂度为 O（n^2）

测试

• 常规测试：n == 某奇数；n == 某偶数
• 边界测试： 当 n == 1 时的特殊案例; n == 20 时，算法是否效率够快

---

总结

• 微软著名旋转矩阵系列题，中规中矩中档难度题。
• 旋转矩阵问题在思路上，解体思路不难分析。
• 此类问题在于处理转角时，最后一个格子不算，从而实现数组不越界又不漏掉格子