「谷歌」圣诞夜 刷 62 ~ 独立的路径
基本信息
- 题号:62
- 题厂:谷歌
- 难度系数:中
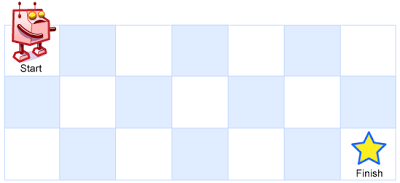
已知一个矩阵,问从起点到终点,一共有几种走法?即图中,粉红机器人走到 finish 星星处,一共有几种不同走法???
例如 m = 3, n = 7 返回 28 —— 种
解题思路
- 机器人只能横走或竖走,即每一次,机器人有两种走法——那我直接写个 recursive 把所有走法遍历出来就好……
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
# 当走到头时,即当前 index 均为 0 时,为一个完整路径走法,返回 path + 1
# 如果还没有,那就有两种走法,向下或向右,分别recursive 直到头
def dfs(down, right, path):
if down == 0 or right == 0:
return path + 1
return dfs(down - 1, right, path) + dfs(down, right - 1, path)
return dfs(m - 1, n - 1, 0)
- 以上代码虽然看起来简洁,但是计算了很多次,是明显会超时的。为了减少冗余的计算,程序届闻风丧胆的动态规划(dynamic programming)闪亮登场了……😭
- 动态规划的思路核心是,一个复杂的结果根植于简单的结果从 1 或 0 开始逐步推导
- 本题中,我们需要倒推思考:
- 如果棋盘只有一个 1 X 1,我们只有一种走法
- 如果棋盘是 2 X 1 或 1 X 2,我们还是只有一种走法,从右往左走,或从下往上走
- 如果棋盘是 2 X 2,我们有了 2 种不同走法,这两种不同走法分别由 2 X 1 和 1 X 2 贡献累加……
- 于是我们推导出:每一个格子的走法 = 左边格子走法 + 右边格子走法
- 让以上思路通过代码实现,我们创建一个与棋盘宽相等的数组 row,初始值为 1。当棋盘为 1 X n,无论 n 取何值,每个格子始终只有一种走法,即向右走……
- 遍历时更新累加值,返回值即 row 的第一个元素
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
row = [1] * n
for i in range(m - 1):
new_row = [1] * n
for j in range(n-2, -1, -1):
new_row[j] = row[j] + new_row[j+1]
row = new_row
return row[0]
Constraints
1 <= m, n <= 100
测试
- 棋盘 1 X 1
- 1 X n 只有一行时
- n X 1 只有一列时
- 100 X 100 取最大值,检验算法有效度
- ……
Big O
时间复杂度:O(n X m), 遍历了每一个格子- 空间复杂度:O(n),创建了长度为 n 的 row 变量
总结
- 考试时遇上,一时想不出动态编程代码,就把 recursive 方法拿去和考官讨论。有解法总比没有强。
- 动态编程困难点有 2:
- 如何找到规律 pattern
- 发现规律后,如何用代码实现此规律解决问题
- 考试时,一时紧张可能很难 40 分钟完成一道动态编程题,但是动态编程系列题模板规律还是挺强的,也就只能熟能生巧解决了……😭