「亚麻」146 ~ 设计 LRC 缓存
基本信息
- 题号:146
- 题厂:亚麻
- 难度系数:中
按题目要求设计一个 LRC 缓存。。。。。。
背景补充:LRC 缓存
LRC(Least Recent Cache):处理缓存的一种算法。当缓存额满时,我们把缓存列表中最久没有使用的缓存移除,留出空位给新的数据缓存。。。。。。
缓存属于系统设计必备考察知识点,而本题只是模拟一下缓存设计。。。。。。
题目要求设计 3 个方法:
- 初始化,确定缓存长度
- 插入(put):如果超额,就把最久没有用到的(LRC)删除
- 获取(get):如果查找的 key 值在缓存中存在 key-value 配对,则返回 value,同时跟新改缓存为最新缓存(most recent cache);如果 key-value 不存在于当前缓存,则返回 -1
例如 ["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"] [[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]] 返回 [null, null, null, 1, null, -1, null, -1, 3, 4]
(案例预示:本题涉及的 key 和 value 全是整数)
解题思路
解决本题的关键问题在于选择何种数据结构??????题目要求 get 和 put 方法的复杂度要控制在 O(1),很容易联想到用 hashmap 存储……
这时除了 hashmap,我们还需要用到双向链表帮忙简化时间复杂度……
- 本题需要设计新的 Node 对象,存储节点 key,value,以及前一个节点和后一个节点;
- 而 hashmap,则对应存储「 key - 节点」 配对;
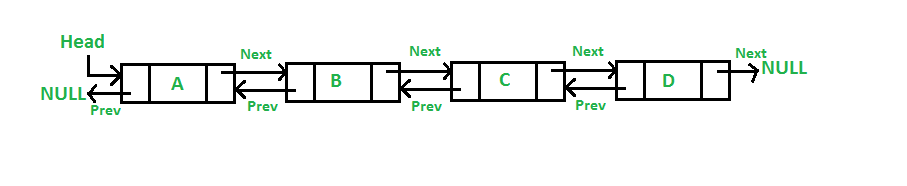
我们模拟两个指针记录双向链表的最左节点和最右节点,左节点的下一节点为最久使用的缓存(least recent),右节点的前一节点为最近使用的缓存(most recent)。
- 如果有新缓存加入,把它插入到最右节点的前面;
- 如果缓存额满需要删除 LRC,把最左边节点的下一个删除即可
# 首先需要设计一下 Node,自带 key,val,prev,nxt 属性
class Node:
def __init__(self, key, val):
self.key = key
self.val = val
self.prev = self.nxt = None
class LRUCache:
def __init__(self, capacity: int):
# 初始化 cache,指明最大额度,
self.capacity = capacity
# 初始记录 key-node 的 hashmap
self.cache = {}
# 初始化左右节点:左节点的下一个是 least recent; 右节点的前一个是 most recent
self.left, self.right = Node(0,0), Node(0, 0)
# 初始化时缓存为空,所以左右节点互相指向
self.left.nxt, self.right.prev = self.right, self.left
# 为了后续方便,创建 insert 和 remove 两个 helper 方法
def insert(self, node: Node):
prev, nxt = self.right.prev, self.right
prev.nxt = nxt.prev = node
node.prev, node.nxt = prev, nxt
def remove(self, node: Node):
prev, nxt = node.prev, node.nxt
prev.nxt, nxt.prev = nxt, prev
def get(self, key: int) -> int:
if key in self.cache:
# 如果当前 key 存在缓存中,我们需要删除,再插入到最右节点前边
self.remove(self.cache[key])
self.insert(self.cache[key])
return self.cache[key].val
return -1
def put(self, key: int, value: int) -> None:
# 跟新缓存时,如果 key 存在于缓存中,需要先删除再更新(添加)
if key in self.cache:
self.remove(self.cache[key])
self.cache[key] = Node(key, value)
self.insert(self.cache[key])
# 当跟新缓存后,发现超额,我们要把最最左边节点的下一个节点删除
if len(self.cache) > self.capacity:
lru = self.left.nxt
del self.cache[lru.key]
self.remove(lru)
Constraints
1 <= capacity <= 30000 <= key <= 1040 <= value <= 105At most 2 * 105 calls will be made to get and put.
测试
- 一个 key 不断跟新 value
- 不断添加新 cache 看 least recent 缓存会不会对应被删除
- ……
Big O
时间复杂度:O(1)- 空间复杂度: O(n)
总结
- 本题为经典算法题,需要反复练习,深入理解
- 本题默认你已知什么是缓存,内存和 SSD 之间的区别,为什么要使用缓存,缓存的基本设计模式……系统设计中缓存必备知识点。考场上,如果你要花 10 分钟和考官讨论啥是 LRC,基本预示本轮歇菜……