「亚麻」289 ~ Game of Life
基本信息
- 题号:289
- 题厂:亚麻
- 难度系数:中
一个 m * n 的矩阵。
左上、上、右上、左、右、左下、下、右下 8 个方位代表邻居。
如果邻居为 1,说明是活邻居,如果邻居为 0,说明是死邻居。
如果 8 个邻居中,活邻居数量少于 2, 那么格子因为人口过少,死了……
如果 8 个邻居中,活邻居数量鉴于 2 ~ 3 之间,那么可以持续延续该格子人口……
如果 8 个邻居中,活邻居数量大于 3,格子因为人口过剩,死了……
如果 8 个邻居中,活邻居数量刚好为 3,格子可以获得重生……
根据以上游戏规则,计算一下棋盘下一代人口分布……
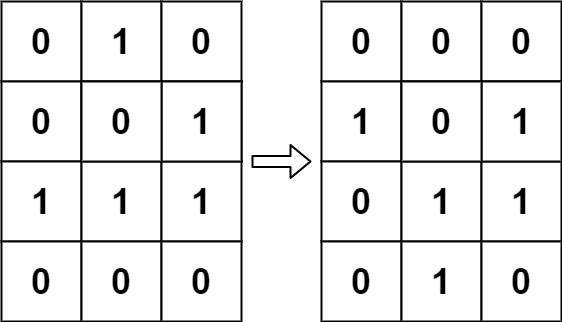
例如 board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]] 返回 [[0,0,0],[1,0,1],[0,1,1],[0,1,0]]
解题思路
- 很明显,首先我们需要遍历矩阵计算一下每个格子对应的活邻居数量。
- 有了活邻居有效数据后,在根据题目规则,决定每个格子的死活(0 或者 1)
题目存在一个比较迷惑的陷阱,「如果 8 个邻居中,活邻居数量鉴于 2 ~ 3 之间,那么可以持续延续该格子人口」。这里的延续人口,就是延续当前格子的数据。
如果格子有 2 个邻居,格子自己为 0,那格子继续为 0;
如果格子有 3 个邻居,格子自己为 1,那格子继续为 1;
但是当格子有 3 个邻居时,无论格子目前是死是活,都自动获得重生……
为了简化以上条件,我们可以理解为:
- 如果 8 个邻居中,活邻居数量少于 2, 无论格子是 0 还是 1,都变成 0
- 如果 8 个邻居中,活邻居数量等于 2 ,无论格子是 0 还是 1,维持现状
- 如果 8 个邻居中,活邻居数量大于 3,无论格子是 0 还是 1,都变成 0
- 如果 8 个邻居中,活邻居数量等于 3,无论格子是 0 还是 1,都变成 1
分析完成之后,这道题还是挺简单的……
class Solution:
def gameOfLife(self, board: List[List[int]]) -> None:
"""
Do not return anything, modify board in-place instead.
"""
# 创建一下棋盘行列数,方便后续
ROW = len(board)
COL = len(board[0])
# 解此题,我们只需要关注活邻居数量,创建一个棋盘用于计数
live_map = [[0] * COL for i in range(ROW)]
# 按照 8 个方向遍历棋盘,计算 活邻居数量
for r in range(ROW):
for c in range(COL):
directions = [(-1, -1), (-1, 0), (-1, 1),
(0, -1), (0, 1),
(1, -1), (1, 0), (1, 1)]
l = 0
for t in directions:
r_neighbor = t[0] + r
c_neighbor = t[1] + c
if (r_neighbor >= 0 and c_neighbor >= 0 and r_neighbor < ROW and c_neighbor < COL):
if board[r_neighbor][c_neighbor] == 1:
l += 1
live_map[r][c] = l
# 根据活邻居数量,判断下一代是死是活……
for r in range(ROW):
for c in range(COL):
if live_map[r][c] < 2:
board[r][c] = 0
elif live_map[r][c] == 3:
board[r][c] = 1
elif live_map[r][c] > 3:
board[r][c] = 0
Constraints
m == board.lengthn == board[i].length1 <= m, n <= 25board[i][j] is 0 or 1.
测试
- n = 1, m = 1 时
- 当整个棋盘全为 1 时
- ……
Big O
时间复杂度:O(m * n)- 空间复杂度: O(m * n)
总结
- 把题目信息分析明白后,本题就是一道在大一编程课 for 循环的基础上加一些花样的题……
- 8 个方向计算邻居数量问题,可以参考各种矩阵问题的方向模板……
到此为止,本题还没有结束,还有 follow up……
- Could you solve it in-place? Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cells.
题目要求进阶一下,在不额外占用内存的情况下计算下一代人口死活
解题思路
- 这种限制内存使用 in-place 的题目,我们很容易想到需要特殊 mark 标记(类似曾经遇到过的 #41, 只不过这一次的数据结构由单维数组升级为双重数组了,但原理还是一样的)
- 题目明确告诉我们,格子就两种数据 0 代表死亡邻居,1 代表活跃邻居。当我们更新下一代人口数量时无非就两种情况:「0 变 1」,「1 变 0」。「0 维持 0」「1 维持 1」的情况不需要考虑。
- 借鉴过往经验,这里我们把 「1 变 0」标记为 「-1」,「0 变 1」标记为 「2」。数邻居数量时,计算格子绝对值为 1 的情况,0 或 2 直接略过……
class Solution:
def gameOfLife(self, board: List[List[int]]) -> None:
"""
Do not return anything, modify board in-place instead.
"""
ROW, COL = len(board), len(board[0])
# 把算邻居提炼成一个 helper 方法
def count_neighbor(r, c):
l = 0
directions = [(-1, -1), (-1, 0), (-1, 1),
(0, -1), (0, 1),
(1, -1), (1, 0), (1, 1)]
for d in directions:
r_nei = r + d[0]
c_nei = c + d[1]
if (r_nei >= 0 and c_nei >= 0 and r_nei < ROW and c_nei < COL):
if abs(board[r_nei][c_nei]) == 1:
l += 1
return l
# 标记 「-1」 1 -> 0
# 标记 「2」 0 -> 1
for r in range(ROW):
for c in range(COL):
l = count_neighbor(r, c)
if l < 2 and board[r][c] != 0:
board[r][c] = -1
elif l == 3 and board[r][c] != 1:
board[r][c] = 2
elif l > 3 and board[r][c] != 0:
board[r][c] = -1
# 计算完成后再标记回去
for r in range(ROW):
for c in range(COL):
if board[r][c] == -1:
board[r][c] = 0
elif board[r][c] == 2:
board[r][c] = 1
总结
- 本题我们复习了矩阵当中涉及的方向坐标查找代码
- 还复习了 in-place 处理中的常见小技巧